题目内容
【题目】某工艺品每件的成本是50元，在某段时间内若以每件x元出售，可卖出(200－2x)件，设这段时间内售出该工艺品的利润为y元．
（1）直接写出利润y(元)与售价x(元)之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大?最大利润是多少？
（3）如果要使利润不低于1200元，且成本不超过2500元，请直接写出x的范围为_____________．
【答案】（1）y=-2x2+300x-10000；（2）单价为75元时，最大利润为1250元；（3）75≤x≤80．
【解析】试题分析：（1）利用销量×每件利润进而得出y与x的函数关系式；
（2）利用二次函数的性质进行进行求解即可；
（3）根据利润不低于1200元，成本不超过2500元，列不等式组进行求解即可.
试题解析：（1）由题意可得：y=（x-50）（200-2x）=﹣2x2+300x－10000；
（2）x=
=75．∵50≤x≤100，∴当x=75时，ymax=1250；
（3）由题意得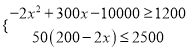
，解得75≤x≤80，
故答案为：75≤x≤80.
练习册系列答案
相关题目
