题目内容
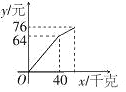
【题目】甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：
根据以上信息，整理分析数据如下：
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 | 4.2 |
（1）写出表格中
，
的值；
（2）从方差的角度看，若选派其中一名参赛，你认为应选哪名队员？并说明理．
【答案】（1）7，7.5；（2）甲，理由略．
【解析】
（1）利用加权平均数的计算公式、中位数的概念解答即可;
（2）根据方差的性质判断即可．
解：∵甲队员的射击成绩为：5,6,6,7,7,7,7,8,8,9,
∴甲队员的射击成绩平均数为：a=(5+6×2+7×4+8×2+9)÷10=7
∵乙队员的射击成绩为：3，6，4，8，7，8，7，8，10，9，从小数到大数依次排列为：3，4，6，7，7，8，8，8，9，10，
∴乙队员射击成绩的中位数为：b=7.5
∴a=7， b=7.5
（2）从方差的角度看，选派甲队员去参赛，理由是：
从表中可知：S甲2=1.2，S乙2=4.2，
∴S甲2＜S乙2
∴甲队员的射击成绩较稳定，
∴选甲队员去参赛
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
