��Ŀ����
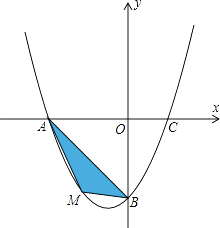
����Ŀ����ͼ�����������Ρ�ABC������AB=AC=25��BC=40������P��B������BC��C�˶����ٶ�Ϊ10��λ/�룮����Q��C������CA��A�˶����ٶ�Ϊ5��λ/�룬��һ���㵽���յ��ʱ��������ͬʱֹͣ�˶�����P���ǵ�P����ֱ��AC�ĶԳƵ㣬����P��P��P��Q�����˶�ʱ��Ϊt�룮
��1������t��ֵΪmʱ��PP��ǡ�þ�����A����m��ֵ��
��2�����P��PQ�����Ϊy����y��t֮��ĺ�����ϵʽ��m��t��4��
��3���Ƿ����ijһʱ��t��ʹPQƽ�ֽǡ�P��PC�����ڣ�����Ӧ��tֵ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��ͼ1�У���AM��BC��M��
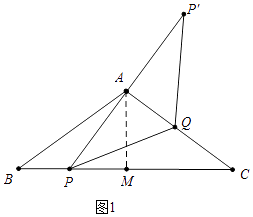
��AB=AC=25��AM��BC��
��BM=MC=20��
��Rt��ABM��AM= ![]() =
= ![]() =15��
=15��
��PP��ǡ�þ�����A����cos��C= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��t= ![]() ��
��
��m= ![]() s
s
��2���⣺��ͼ2�У���PP�佻AC��N��
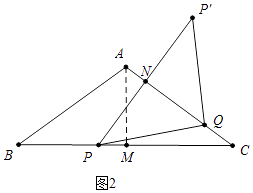
�� ![]() ��t��4ʱ���ɡ�PCN�ס�ACM���ɵ�PC=40��10t��PN=P��N=24��6t��CN=32��8t��
��t��4ʱ���ɡ�PCN�ס�ACM���ɵ�PC=40��10t��PN=P��N=24��6t��CN=32��8t��
��CQ=5t��
��NQ=CN��CQ=32��13t��
��y= ![]() PP��NQ=
PP��NQ= ![]() ��48��12t����32��13t��=78t2��504t+768��
��48��12t����32��13t��=78t2��504t+768�� ![]() ��t��4��
��t��4��
��3���⣺���ڣ��������£�
��ͼ3�У���QE��BC��E��
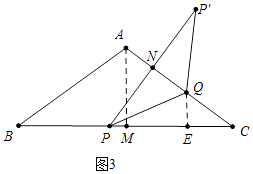
��PQƽ�֡�CPP�䣬QE��PC��QN��PP�䣬
��QN=QE��
��sin��C= ![]() =
= ![]() ��
��![]()
��t=2��
��t=2ʱ��PQƽ�ֽǡ�P��PC
����������1���ɡ�C�����Ҷ������Rt��APC���ֿ���Rt��ACM���г�����ʽ��������ȣ��������̣����m;��2���ɡ�PCN�ס�ACM,�ɱ�ʾ��PC=40��10t��PN=P��N=24��6t,CN=32��8t�����������ʽ�����ɵ�y= ![]() PP��NQ=78t2��504t+768;��3�����á�C�����������ֱ�ʾ�ı���ʽ��������ȣ����г�����,���t.
PP��NQ=78t2��504t+768;��3�����á�C�����������ֱ�ʾ�ı���ʽ��������ȣ����г�����,���t.
�����㾫����������Ҫ���������������ε��ж������ʺ�������Ǻ����Ķ�������֪ʶ�㣬��Ҫ�������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������A�����ҡ����ҡ����С����ж�������A��������Ǻ���������ȷ�����⣮

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ��Ƴ���������ͳ��ͼ��

����������Ϣ�����������������£�
ƽ���ɼ�/�� | ��λ��/�� | ����/�� | ���� | |
�� |
| 7 | 7 | 1.2 |
�� | 7 |
| 8 | 4.2 |
��1���������![]() ��
��![]() ��ֵ��
��ֵ��
��2���ӷ���ĽǶȿ�����ѡ������һ������������ΪӦѡ������Ա����˵������
����Ŀ��Ϊ�����ѧ��������д����������ǿ�������ֵ���ʶ��ijУ�ٰ����조������д��������ѧ����ѡ�κ������������Է����ǣ���д100�����֣�ÿ��ȷ��д��һ�����ֵ�1�֣����ξ�����ѧ���ɼ�Ϊx���֣�����50��x��100�����䰴�����η�Ϊ���飬���Ƴ����²���������
��� | �ɼ�x���֣� | Ƶ���������� | Ƶ�� |
һ | 50��x��60 | 2 | 0.04 |
�� | 60��x��70 | 10 | 0.2 |
�� | 70��x��80 | 14 | b |
�� | 80��x��90 | a | 0.32 |
�� | 90��x��100 | 8 | 0.16 |
����ݱ����ṩ����Ϣ������������⣺
��1��ֱ��д������a= �� b=��
��2���벹ȫ������Ӧ��Ƶ���ֲ�ֱ��ͼ��
��3���������ɼ�������80��Ϊ���㣬�δ�����������Ϊ ��
��4������ݵõ���ͳ�����ݣ���Ҫ������Щͬѧ�ĺ�����д��������Ϊ���ͬѧ�ǵ���д����������һ�����飨���Ὠ�鲻����20�֣�