题目内容
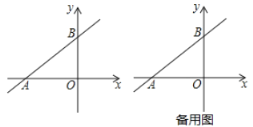
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且经过点
两点,且经过点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
,
①求![]() 的值;
的值;
②点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 为坐标平面内另一点,若以
为坐标平面内另一点,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形,请直接写出所有符合条件的点
为顶点的四边形是菱形,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①3;②
;(2)①3;②![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点(4,b+3)代入直线解析式中即可得出结论;
(2)①先求出点A,B坐标,进而得出AB,再利用AB=OB+2,即可求出b;
②分三种情况利用菱形的性质即可得出结论.
解:(1)直线y=kx+b经过点(4,b+3)
∴4k+b=b+3,
∴4k=3,
∴k=![]()
(2)①由(1)知A,B在y=![]() x+b上,
x+b上,
当x=0时,y=b, ∴B(0,b),
当y=0时,![]() x+b=0,解得x=
x+b=0,解得x=![]() ∴A(
∴A(![]() ,0),
,0),
∴OA=![]() ,OB=b
,OB=b
∴AB=![]()
∵AB=OB+2
∴![]() =b+2
=b+2
∴b=3
故答案为:3
②如图,由①知,b=3,∴A(-4,0),B(0,3) ∴AB=5
∵以A,B,M,N为顶点的四边形是菱形,
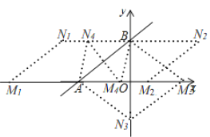
所以,分3种情况:
Ⅰ、当AB与AM为两邻边时,BN∥AM,BN=AM=AB=5,
∴N(-5,3)或(5,3)
Ⅱ、当AB与BM为两邻边时,AM和AN是对角线,∵B(0,3) ∴N(0,-3),
Ⅲ、当AM和AN为两邻边时,BN∥AM,
设N(n,3),∴BM=AM=BN=﹣n ∴OM=4+n,
根据勾股定理得,n2-(4+n)2=9,
n=﹣![]()
N(﹣![]() ,3)
,3)
故答案为:N(5,3)或(-5,3)或(0,-3)或(﹣![]() ,3)
,3)

练习册系列答案
相关题目
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 | 4.2 |
(1)写出表格中![]() ,
,![]() 的值;
的值;
(2)从方差的角度看,若选派其中一名参赛,你认为应选哪名队员?并说明理.