题目内容
【题目】如图,张大爷用32米长的篱笆围成一个矩形菜园,菜园一边靠墙(墙长为15米),平行于墙的一面开一扇宽度为2米的门,张大爷还在菜园内开辟出一个小区域存放化肥,两个区域用篱笆隔开,并有一扇2米的门相连(注:所有门都用其它材料).
(1)设平行于墙的一边长度为y米,垂直于墙的一边长度为x米,直接写出y与x的函数关系式,并写出自变量x的取值范围;
(2)设此时整个菜园的面积为Sm2(包括化肥存放处),则S的最大值为多少?
(3)若此时整个菜园的面积不小于81m2(包括化肥存放处),结合图象,直接写出x的取值范围.

【答案】(1)![]() (
(![]() );(2)105
);(2)105![]() ;(3)
;(3)![]()
【解析】
(1)根据矩形的周长与长、宽的关系,可得答案;
(2)根据矩形的面积,可得函数解析式,根据二次函数的性质,可得函数的最大值;
(3)先令面积等于81,求出两个解,根据函数的图象,可得自变量的取值范围.
解:(1)由题意得长和宽的总和为![]() (米)
(米)
∴![]()
根据题意有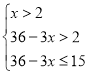 解得
解得![]()
∴![]() (
(![]() )
)
(2)由题意得![]()
∴当x=7时,S的值最大,最大值=105![]() .
.
(3)令S=81,即![]()
解得x=3或x=9,
如图:
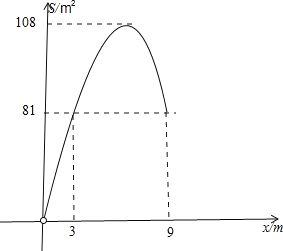 ,
,
由图象得出x的取值范围:3≤x≤9.
又∵![]()
∴![]()

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目