题目内容
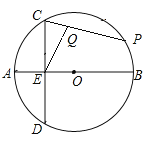
【题目】如图,C为圆O上一动点(不与点B重合),点T为圆O上一动点,且∠BOT=60°,将BC绕点B顺时针旋转90°得到BD,连接TD,当TD最大时,∠BDT的度数为_____.
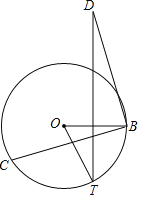
【答案】7.5°
【解析】
作与圆O半径相等的圆E,圆E与圆O的直径AB相切与点B,连接TE并延长交圆E于点D,连接BD,作BC⊥BD,交圆O于点C,则BE⊥AB,在圆E上取一点F,连接TF、EF,则TE+EF>TF,由DE=EF,得出TD>TF,此时TD最大,易证△OBT是等边三角形,得出∠OBT=60°,BT=OB=BE,求出∠EBT=90°+60°=150°,∠BET=![]() (180°﹣150°)=15°,∠EDB=
(180°﹣150°)=15°,∠EDB=![]() ∠BET=7.5°,即可得出结果.
∠BET=7.5°,即可得出结果.
解:作与圆O半径相等的圆E,圆E与圆O的直径AB相切与点B,连接TE并延长交圆E于点D,连接BD,作BC⊥BD,交圆O于点C,如图所示:
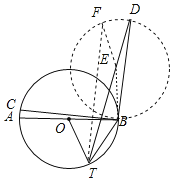
则BE⊥AB,
在圆E上取一点F,连接TF、EF,则TE+EF>TF,
∵DE=EF,
∴TD>TF,
∴此时TD最大,
∵OB=OT,∠BOT=60°,
∴△OBT是等边三角形,
∴∠OBT=60°,BT=OB=BE,
∴∠BET=∠BTE,
∵BE⊥AB,
∴∠EBT=90°+60°=150°,
∴∠BET=![]() (180°﹣150°)=15°,
(180°﹣150°)=15°,
∵ED=EB,
∴∠EDB=∠EBD,
∴∠EDB=![]() ∠BET=
∠BET=![]() ×15°=7.5°,
×15°=7.5°,
即∠BDT的度数为7.5°,
故答案为:7.5°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目