题目内容
【题目】嘉嘉和琪琪在用一副三角尺研究数学问题:
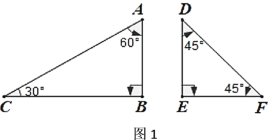
一副三角尺分别有一个角为直角,其余角度如图1所示,![]() .
.
发现:
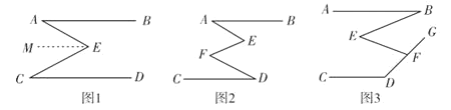
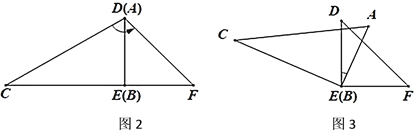
(1)如图2,当![]() 与
与![]() 重合时,
重合时,![]() _____.
_____.
(2)如图3,将图2中![]() 绕
绕![]() 点顺时针旋转一定角度使得
点顺时针旋转一定角度使得![]() ,求
,求![]() 的度数.
的度数.
拓展:
(3)如图4,继续旋转,使得![]() 于点
于点![]() ,
,
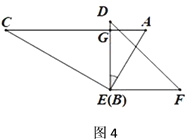
①此时![]() 与
与![]() 平行吗?请说明理由.
平行吗?请说明理由.
②求![]() 的度数.
的度数.
探究:
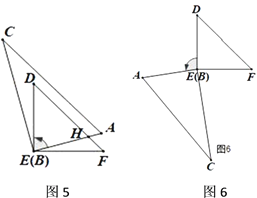
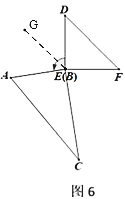
(4)如图5、图6,继续旋转,使得![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①平行,垂直于同一条直线的两条直线平行;②
;(3)①平行,垂直于同一条直线的两条直线平行;②![]() ;(4)
;(4)![]() ,
,![]() ;
;
【解析】
(1)利用角的和差关系计算即可;(2)利用角的和差关系计算即可;(3)①根据平行线的判定定理即可得答案;②利用直角三角形两锐角互余的性质即可得答案;(4)在图5中,根据平行线的性质可得∠DHE的度数,根据三角形内角和定理即可求出∠AED的度数,在图6中,过E作EG//AC,根据平行线的性质即可得∠AED的度数.
(1)∵∠CAB=60°,∠EDF=45°,
∴∠CDF=∠CAB+∠EDF=105°,
(2)∵![]() ,∠CBA=90°,∠DEF=90°,
,∠CBA=90°,∠DEF=90°,
∴∠CBA+∠AEB=∠CBA+∠DEF-∠AED=90°+90°-∠AED=156°,
∴∠AED=180°-156°=24°.
(3)①平行,理由如下:
∵![]() ,∠DEF=90°,
,∠DEF=90°,
∴AC//EF.
②∵![]() ,∠C=30°,
,∠C=30°,
∴∠CED=90°-30°=60°,
∵∠CBA=90°,
∴∠AED=90°-60°=30°,
(4)在图5中,
∵AC//EF,
∴∠DHE=∠A=60°,
∵∠D=45°,
∴∠AED=180°-60°-45°=75°,
在图6中,过过E作EG//AC,
∵AC//DF,EG//AC,
∴EG//DF,
∴∠DEG=∠D=45°,∠AEG=∠A=60°,
∴∠AED=45°+60°=105°,

 名校课堂系列答案
名校课堂系列答案【题目】世界上大部分国家都使用摄氏温度(![]() ),但美国、英国等国家的天气预报仍然使用华氏温度(
),但美国、英国等国家的天气预报仍然使用华氏温度(![]() ).两种计量之间有如下对应:
).两种计量之间有如下对应:
摄氏温度( |
|
|
|
|
|
|
华氏温度( |
|
|
|
|
|
|
(1)上表反映了哪两变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(![]() )每提高
)每提高![]() 度,华氏温度(
度,华氏温度(![]() )提高_____度.
)提高_____度.
(3)摄氏温度![]() 度时华氏温度为______度.
度时华氏温度为______度.
(4)华氏温度![]() 度时摄氏温度为_______度.
度时摄氏温度为_______度.
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.