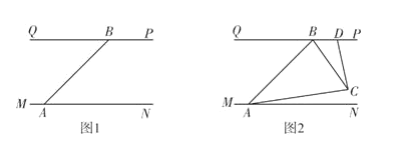��Ŀ����
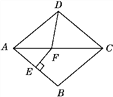
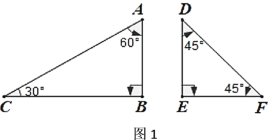
����Ŀ�������龳����ͼ1��AB��CD����A=30�㣬��C=40�㣬���AEC�Ķ���.С����˼·�ǣ�

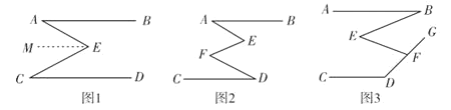
��1���������ԣ���С����˼·����á�AEC�Ķ�����
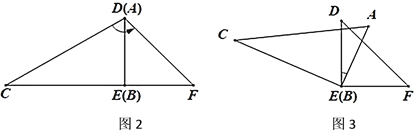
��2������Ǩ�ƣ���ͼ2��AB��CD����E��FΪAB��CD�ڲ����㣬�ʡ�A����E����F�͡�D֮���к�������ϵ?��˵�����ɣ�
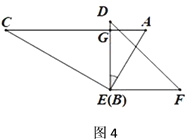
��3��Ӧ����չ����ͼ3��AB��CD����E��FΪAB��CD�ڲ����㣬�����E+��EFG=160�㣬��ֱ��д����B���D֮�ʵ�������ϵ.
���𰸡���1��70�� ��2���𰸼����� ��3����B+��D=160��
��������
��1�����Ӹ����ߣ�ת������ͼ�Σ���E��EM��AB������ƽ���ߵ����ʿ�֤�á�A =��AEM����C=��CEM����֤����AEC=��A+��C���̶��ɽ�����⣻
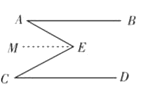
��2�����Ӹ����ߣ�ת����ֱ��ƽ�еĻ���ͼ�Σ�����E��EM��AB, ����F��FN��AB ������ƽ���ߵ����ʿ�֤AB��ME��FN��CD�� �ٸ�����ֱ��ƽ�У��ڴ�����ȣ���֤�á�A =��AEM����MEF=��EFN,��D=��DFN��Ȼ����ʽ��ӣ���֤�ý��ۣ�
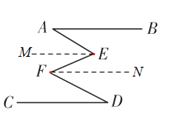
��3������E��EH��AB������F��FM��AB �������֪��֤��AB��CD��FM��EH��������ֱ��ƽ�У�ͬλ����ȣ�ͬ���ڽǻ�������֤��B=��BEH����EFM=��HEF����MFD+��D=180�㣬�ٽ�������ʽ��ӣ������ɵõ���B+��D=180��+��BEF-��EFD��Ȼ���ɡ�BEF+��EFG=160�� �����Ƴ���BEF-��EFD=-20�㣬������������B+��D��ֵ.
��1����ͼ����E��EM��AB��
��AB��CD����AB��ME��CD��
���A =��AEM����C=��CEM��
���AEC=��A+��C=70�㣻
��2����A+��EFD =��AEF+��D
�������£�����E��EM��AB, ����F��FN��AB
��AB��CD����AB��ME��FN��CD��
���A =��AEM����MEF=��EFN,��D=��DFN��
���A+��EFD =��AEF+��D��
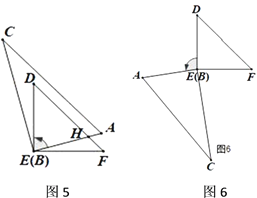
��3������E��EH��AB������F��FM��AB ��

��AB��CD��
��AB��CD��FM��EH��
���B=��BEH����EFM=��HEF����MFD+��D=180�㣬
���B+��EFM+��MFD+��D=180��+��BEH+��HEF��
���B+��D+��EFD=180��+��BEF��
���B+��D=180��+��BEF-��EFD��
�� ��BEF+��EFG=160�� ��
���BEF+180��-��EFD=160�㣬
���BEF-��EFD=-20�㣬
���B+��D=180��-20��=160��.

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�