题目内容
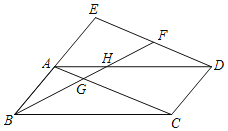
【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使得AE=AB,联结DE、AC.点F在线段DE上,联结BF,分别交AC、AD于点G、H.
(1)求证:BG=GF;
(2)如果AC=2AB,点F是DE的中点,求证:AH2=GHBH.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由平行四边形的性质可得AB=CD=AE,AB∥CD,可证四边形ACDE是平行四边形,可得![]() ,可得结论;
,可得结论;
(2)由“SAS”可证△BEF≌△DEA,可得∠EBF=∠EDA,通过证明△AHG∽△BHA,可得结论.
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB=AE,
∴AE=CD,
∴四边形ACDE是平行四边形,
∴AC∥DE,
∴![]() ,
,
∴BG=GF;
(2)∵AB=AE,
∴BE=2AE,
∵AC=2AB,
∴BE=AC,
∵四边形ACDE是平行四边形,
∴AC=DE,
∴DE=BE,
∵点F是DE的中点,
∴DE=2EF,
∴AE=EF,
∵DE=BE,∠E=∠E,AE=EF,
∴△BEF≌△DEA(SAS),
∴∠EBF=∠EDA,
∵AC∥DE,
∴∠GAH=∠EDA.
∴∠EBF=∠GAH.
∵∠AHG=∠BHA,
∴△AHG∽△BHA,
∴![]() .
.
∴AH2=GHBH.

【题目】甲、乙两校各选派10名学生参加“美丽泰州乡土风情知识”大赛预赛.各参赛选手的成绩如下:
甲校:93,98,89,93, 95,96, 93,96,98, 99;
乙校:93,94,88,91,92,93,100, 98,98,93.
通过整理,得到数据分析表如下:
学校 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
甲校 | 99 | a | 95.5 | 93 | 8.4 |
乙校 | 100 | 94 | b | 93 | c |
(1)填空:a = ,b = ;
(2)求出表中c的值,你认为哪所学校代表队成绩好?请写出两条你认为该队成绩好的理由.
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3