题目内容
【题目】如图，点E为矩形ABCD的边BC长上的一点，作DF⊥AE于点F，且满足DF=AB．下面结论：①△DEF≌△DEC；②S△ABE = S△ADF；③AF=AB；④BE=AF．其中正确的结论是（ ）
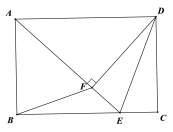
A.1个B.2个C.3个D.4个
【答案】C
【解析】
证明Rt△DEF≌Rt△DEC得出①正确；在证明△ABE≌△DFA得出S△ABE＝S△ADF；②正确；得出BE＝AF，④正确，③不正确；即可得出结论．
解：∵四边形ABCD是矩形，
∴∠C＝∠ABE＝90°，AD∥BC，AB＝CD，
∵DF＝AB，
∴DF＝CD，
∵DF⊥AE，
∴∠DFA＝∠DFE＝90°，
在Rt△DEF和Rt△DEC中，
，
∴Rt△DEF≌Rt△DEC（HL），①正确；
∵AD∥BC，
∴∠AEB＝∠DAF，
在△ABE和△DFA中，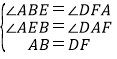
，
∴△ABE≌△DFA（AAS），
∴S△ABE＝S△ADF；②正确；
∴BE＝AF，④正确，③不正确；
正确的结论有3个，
故选：C．
练习册系列答案
名校课堂系列答案
相关题目
