题目内容
【题目】已知二次函数y=ax2+bx+c的图象经过A(n,b),B(m,a)且m+n=1.
(1)当b=a时,直接写出函数图象的对称轴;
(2)求b和c(用只含字母a、n的代数式表示):
(3)当a<0时,函数有最大值-1,b+c≥a,n≤![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ≤a≤
≤a≤![]() .
.
【解析】
(1)用抛物线对称轴公式求解;
(2)将A(n,b),B(m,a)代入解析式,用待定系数法求解;
(3)由b+c的值列不等式求得n的取值范围,然后将二次函数配方为顶点式后根据题意可得![]() ,然后将b和c代入化简求得
,然后将b和c代入化简求得![]() ,然后根据n的取值范围求得a的取值范围.
,然后根据n的取值范围求得a的取值范围.
解:(1)由题意可得
抛物线的对称轴为:直线![]()
(2)因为二次函数![]() 经过A(n,b),B(m,a),
经过A(n,b),B(m,a),
所以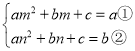
方程组①-②,得
![]() ,
,
![]() ,
,
∵m-n=1, a![]() ,
,
∴![]() ,
,
得![]() ,
,
把![]() 代入方程组中②,得
代入方程组中②,得
![]() ,
,
(3)由(2)可知:![]()
又![]()
![]() ≥a
≥a
![]()
![]() ≥a,
≥a,
当a<0时,n≥![]() ,
,
由n≤![]() 得,
得,![]() ≤n≤
≤n≤![]() ,
,
∵![]() ,a<0
,a<0
![]()
![]()
![]()
![]() ,且
,且![]() ,得
,得
![]() ,
,
化简得,![]() ,
,
∴![]() ,
,
配方得![]() ,
,
∵![]() 在
在![]() ≤n≤
≤n≤![]() 时随n的增大而增大
时随n的增大而增大
![]() 当n=
当n=![]() 时,
时,![]() ,当n=
,当n=![]() 时,
时,![]()
![]()
![]()
![]() ≤a≤
≤a≤![]() .
.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目