题目内容
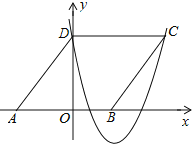
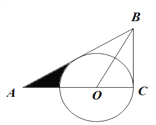
【题目】如图,△ABC中,∠C=90,∠ABC=2∠A,点O在AC上,OA=OB,以O为圆心,OC为半径作圆.
(1)求证:AB是⊙O的切线;
(2)若BC=3,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]()
![]() -
-![]() π.
π.
【解析】
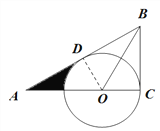
(1)、作OD⊥AB,垂足为D,根据已知中的角度之间的关系得出OD=OC,从而得出切线;(2)、利用△AOD的面积减去扇形的面积得出阴影部分的面积.
(1)、作OD⊥AB,垂足为D. ∵∠C=90,∠ABC=2∠A,∴∠A=30°,∠ABC=60°,
∵OA=OB, ∴∠OBA=∠A=30,∴∠OBC=30°, ∴∠OBA=∠OBC,
∴OD=OC,∴AB是⊙O的切线
(2)、∵∠A=30°,BC=3,∴sinA=![]() , ∴AB=6,AC=
, ∴AB=6,AC=![]() , ∵OD=OC=
, ∵OD=OC=![]() AO,
AO,
∴OD=![]() , ∴AO=2
, ∴AO=2![]() ,AD=3, ∴S△AOD=
,AD=3, ∴S△AOD=![]() ×
×![]() ×3=
×3=![]()
![]() ,S扇形=
,S扇形=![]() =
=![]() π,
π,
∴S阴影=![]()
![]() -
-![]() π.
π.

练习册系列答案
相关题目
【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
![]()
成绩段 | 频数 | 频率 |
0≤x<20 | 5 | 0.1 |
20≤x<40 | 10 | a |
40≤x<60 | b | 0.14 |
60≤x<80 | m | c |
80≤x<100 | 12 | n |
![]()
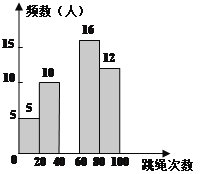
根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多人?