题目内容
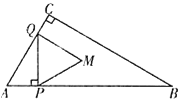
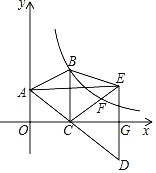
【题目】如图,在△ABC中,AB=AC,点A在y轴上,点C在x轴上,BC⊥x轴,tan∠ACO=![]() .延长AC到点D,过点D作DE⊥x轴于点G,且DG=GE,连接CE,反比例函数y=
.延长AC到点D,过点D作DE⊥x轴于点G,且DG=GE,连接CE,反比例函数y=![]() (k≠0)的图象经过点B,和CE交于点F,且CF:FE=2:1.若△ABE面积为6,则点D的坐标为_____.
(k≠0)的图象经过点B,和CE交于点F,且CF:FE=2:1.若△ABE面积为6,则点D的坐标为_____.
【答案】(![]() ,﹣3).
,﹣3).
【解析】
根据AB=AC,tan∠ACO=![]() ,设未知数表示点A、B、C的坐标,根据线段中垂线的性质得CE=CD,进而得到∠ECG=∠DCG=∠ACO,再根据tan∠ECG=tan∠ACO=
,设未知数表示点A、B、C的坐标,根据线段中垂线的性质得CE=CD,进而得到∠ECG=∠DCG=∠ACO,再根据tan∠ECG=tan∠ACO=![]() ,再设未知数表示出点E的坐标,进而求出CE的中点F的坐标,把点B、F的坐标代入反比例函数的关系式,进而得出两个未知数之间的关系,再根据
,再设未知数表示出点E的坐标,进而求出CE的中点F的坐标,把点B、F的坐标代入反比例函数的关系式,进而得出两个未知数之间的关系,再根据![]() =6,列方程求出未知数,进而确定点的坐标.
=6,列方程求出未知数,进而确定点的坐标.
解:过点A作AM⊥BC,垂足为M,
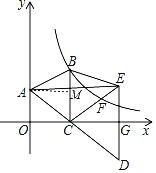
∵AB=AC,
∴BM=CM,
∵tan∠ACO=![]() =
=![]() .
.
∴设OA=2m,OC=3m,则BC=4m,因此点C(3m,0)、B(3m,4m),
∵DE⊥x轴于点G,且DG=GE,
∴CE=CD,
∴∠ECG=∠DCG=∠ACO,
∴tan∠ECG=![]() =tan∠ACO=
=tan∠ACO=![]() ,
,
设EG=2n,则CG=3n,因此点E(3m+3n,2n),
又∵CF:FE=2:1.即点F是CE的三等分点,
∴点F(3m+2n,![]() n),
n),
把B(3m,4m)和F(3m+2n,![]() n)代入反比例函数y=
n)代入反比例函数y=![]() 得,
得,
k=3m4m=(3m+2n)![]() n,即(3m﹣2n)(3m+n)=0,
n,即(3m﹣2n)(3m+n)=0,
∵m>0,n>0,
∴n=![]() m,
m,
∴点E的坐标为(![]() m,3m),
m,3m),
∵S△ABE=6=S梯形ABCO+S梯形BCGE﹣S梯形AOGE,
∴![]() (2m+4m)×3m+
(2m+4m)×3m+![]() (4m+3m)×
(4m+3m)×![]() m﹣
m﹣![]() (2m+3m)×
(2m+3m)×![]() m=6,
m=6,
解得:m=1,
∴E(![]() ,3),
,3),
∴D(![]() ,﹣3)
,﹣3)
故答案为:(![]() ,﹣3).
,﹣3).

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目