Question

【题目】请阅读下列材料，并完成相应的任务．

三等分任意角问题是数学史上一个著名的问题，直到1837年，数学家才证明了“三等分任意角”是不能用尺规完成的．

在探索中，出现了不同的解决问题的方法

方法一：

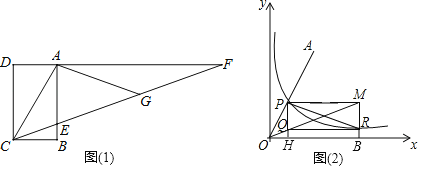
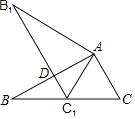
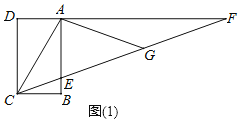
如图（1），四边形ABCD是矩形，F是DA延长线上一点，G是CF上一点，CF与AB交于点E，且∠ACG＝∠AGC，∠GAF＝∠F，此时∠ECB＝∠ACB．

方法二：

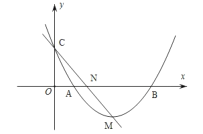
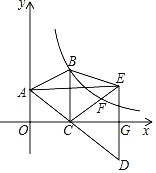
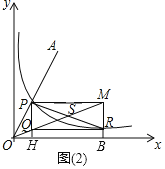
数学家帕普斯借助函数给出一种“三等分锐角”的方法（如图（2））：将给定的锐角∠AOB置于平面直角坐标系中，边OB在x轴上，边OA与函数y＝的图象交于点P，以点P为圆心，以2OP长为半径作弧交图象于点R．过点P作x轴的平行线，过点R作y轴的平行线，两直线相交于点M，连接OM得到∠AOB，过点P作PH⊥x轴于点H，过点R作RQ⊥PH于点Q，则∠MOB＝∠AOB．

（1）在“方法一”中，若∠ACF＝40°，GF＝4，求BC的长．

（2）完成“方法二”的证明．

Answer 1

【答案】（1）2；（2）证明见解析.

【解析】

（1）先求出AC的值再求出∠ACB，利用三角函数即可解答

（2）设点P的坐标为（a，），点R的坐标为（b，），则点Q的坐标为（a，），点M的坐标为（b，），求出直线OM的解析式，得出四边形PQRM为矩形，设PR交MQ于点S，根据SP＝SQ＝SR＝SM＝PR，即可解答

（1）解：∵∠ACG＝∠AGC，∠GAF＝∠F，

∴AC＝AG＝GF＝4．

∵∠ECB＝ ∠ACB，∠ACF＝40°，

∴∠ACB＝ ∠ACF＝60°，

∴BC＝ACcos∠ACB＝4×＝2．

（2）证明：设点P的坐标为（a，），点R的坐标为（b，），则点Q的坐标为（a，），点M的坐标为（b，）．

设直线OM的解析式为y＝kx（k≠0），

将M（b，）代入y＝kx，得：＝kb，

∴k＝，

∴直线OM的解析式为y=x．

∵当x＝a时，y＝，

∴点Q在直线OM上．

∵PH⊥x轴，RQ⊥PH，MP∥x轴，MR∥y轴，

∴四边形PQRM为矩形．

设PR交MQ于点S，如图（2）所示．

则SP＝SQ＝SR＝SM＝PR，

∴∠SQR＝∠SRQ．

∵PR＝2OP，

∴PS＝OP＝PR，

∴∠POS＝∠PSO．

∵∠PSQ＝2∠SQR，

∴∠POS＝2∠SQR．

∵RQ∥OB，

∴∠MOB＝∠SQR，

∴∠POS＝2∠MOB，

∴∠MOB＝∠AOB．