Question

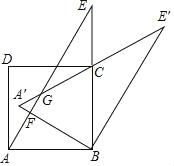
【题目】连接正八边形的三个顶点，得到如图所示的图形，下列说法错误的是（ ）

A. 是等边三角形

B. 连接，则分别平分和

C. 整个图形是轴对称图形，但不是中心对称图形

D. 四边形与四边形的面积相等

Answer 1

【答案】A

【解析】

由正八边形的性质得出A不正确，B、C、D正确，即可得出结论．

∵八边形ABCDEFGH是正八边形，

∴AB=CB=AH=GH=GF=EF=DE=CD，AF=CF，∠AFC=90°-45°=45°，

∴∠FAC=∠FCA=（180°-45°）=67.5°，

∴△ACF不是等边三角形，选项A错误；

∵正八边形是轴对称图形，直线BF是对称轴，

∴连接BF，则BF分别平分∠AFC和∠ABC，

∴选项B、C正确；

∵四边形AFGH与四边形CFED的面积相等，

∴选项D正确；

故选A．