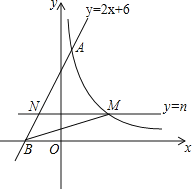题目内容
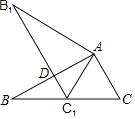
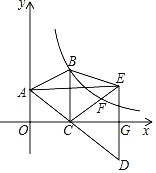
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发以每秒2个单位的速度沿
出发以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() ,当点
,当点![]() 不和
不和![]() 的顶点重合时,以
的顶点重合时,以![]() 为边作等边三角形
为边作等边三角形![]() ,使点
,使点![]() 和点
和点![]() 在直线
在直线![]() 的同侧,设点
的同侧,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)求等边三角形![]() 的边长(用含
的边长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边
的边![]() 上时,求
上时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)作直线![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,直接写出
,直接写出![]() 时
时![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ;(4)
;(4)![]() 的值为
的值为![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)分两种情况讨论:当点Q在线段AC上时,当点Q在线段BC上时,根据30度的直角三角形的性质或特殊的三角函数列式可得结论;
(2)根据PQ=PM,列出关于t的方程即可解答;
(3)分三种情况:①当![]() 时,Q在AC上,如图2,△PQM与△ABC重合部分图形是等边△PMQ,
时,Q在AC上,如图2,△PQM与△ABC重合部分图形是等边△PMQ,
②当![]() 时,Q在BC上,如图5,△PQM与△ABC重合部分图形是四边形PEDQ,
时,Q在BC上,如图5,△PQM与△ABC重合部分图形是四边形PEDQ,
③当![]() 时,Q在BC上,如图4,△PQM与△ABC重合部分图形是等边△PMQ,
时,Q在BC上,如图4,△PQM与△ABC重合部分图形是等边△PMQ,
根据面积公式可得结论;
(4)分两种情况:
①当Q在AC上时,如图6,根据AC=AQ+CQ,列关于t的方程可得结论;
当Q在BC上时,如图7,根据CQ=Q'E=2PQ,列关于t的方程可得结论.
解:(1)由题意,得![]() ,在
,在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,当点
,当点![]() 与点
与点![]() 重合时,如图①,
重合时,如图①,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,当点
,当点![]() 在边
在边![]() 上时,如图②,
上时,如图②,
即![]()
当点![]() 在边
在边![]() 上时,如图③,即
上时,如图③,即![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)当点![]() 落在
落在![]() 上时,如图④,
上时,如图④,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
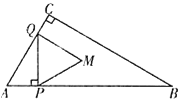
(3)分三种情况:①当![]() 时,点
时,点![]() 在
在![]() 上,如图②,
上,如图②,![]() 与
与![]() 重合部分图形是等边
重合部分图形是等边![]() ,
,
∴![]() ;
;
②当![]() 时,点
时,点![]() 在
在![]() 上,如图⑤,
上,如图⑤,![]() 与
与![]() 重合部分图形是四边形
重合部分图形是四边形![]() ,
,
由(2)得,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴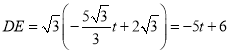 ,
,
∴![]()
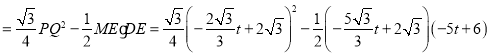
![]()
③当![]() 时,点
时,点![]() 在
在![]() 上,如图④,
上,如图④,![]() 与
与![]() 重合部分图形是等边
重合部分图形是等边![]() ,
,
∴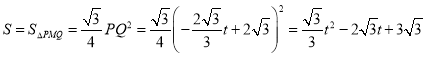
综上所述,![]() 与
与![]() 的函数关系式为
的函数关系式为
(4)分两种情况:
①当点![]() 在
在![]() 上时,如图⑥,
上时,如图⑥,![]() ,延长
,延长![]() 、
、![]() 交
交![]() 于同一点
于同一点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由对称得:![]() ,
,
∴![]() ,
,![]() 中,
中,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
②当点![]() 在
在![]() 上时,如图⑦,当
上时,如图⑦,当![]() 时,点
时,点![]() 在
在![]() 上,连接
上,连接![]() ,并延长
,并延长![]() 、
、![]() 交
交![]() 上同一点为
上同一点为![]() ,易得
,易得![]() ,
,
∴![]() ,由(2)知
,由(2)知![]() ,
,
∴![]() ,由
,由![]() 得
得![]() ,
,
解得![]() ,则
,则![]() 时
时![]() 的值为
的值为![]() 秒或
秒或![]() 秒.
秒.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案