��Ŀ����
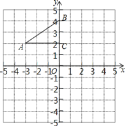
����Ŀ��С���о����κ���y=-(x-m)2-m+1(mΪ����)����ʱ���½��ۣ����������ͼ��Ķ���ʼ����ֱ��y=-x+1�ϣ��ڴ���һ��m��ֵ��ʹ�ú���ͼ��Ķ�����![]() ����������㹹�ɵ���ֱ�������Σ��۵�A(x1,y1)���B(x2,y2)�ں���ͼ���ϣ���x1<x2��x1+x2>2m����y1<y2���ܵ�-1<x<2ʱ��y��x�������������m��ȡֵ��ΧΪm��2���д�����۵�����ǣ� ��
����������㹹�ɵ���ֱ�������Σ��۵�A(x1,y1)���B(x2,y2)�ں���ͼ���ϣ���x1<x2��x1+x2>2m����y1<y2���ܵ�-1<x<2ʱ��y��x�������������m��ȡֵ��ΧΪm��2���д�����۵�����ǣ� ��
A. ��B. ��C. ��D. ��
���𰸡�C
��������
�Ѷ����������y=-x+1�����жϢ٣����ݹ��ɶ��������жϢڣ������ڶԳ�����ұ�y��x���������С���жϢۣ��������ڶԳ�����ұ�y��x�������������жϢ�.
�ѣ�m��-m+1������y=-x+1��-m+1=-m+1����=�ң��ʢ���ȷ��
��-(x-m)2-m+1=0ʱ��x1=![]() , x2=
, x2=![]() ,
,
��������![]() ����������㹹�ɵ���ֱ�������Σ�
����������㹹�ɵ���ֱ�������Σ�
��1-m+(1-m)2+1-m+(1-m)2=4(1-m)����m2-m=0��
��m=0��1ʱ�������һ��m��ֵ��ʹ�ú���ͼ��Ķ�����![]() ����������㹹�ɵ���ֱ�������Σ��ʢ���ȷ��
����������㹹�ɵ���ֱ�������Σ��ʢ���ȷ��
��x1<x2����x1��x2�ڶԳ����Ҳ�ʱ��
��-1<0, ���ڶԳ����Ҳ�y��x���������С����y1>y2���ʢ۴���
��-1<0, ���ڶԳ������y��x�����������
��m��2���ʢ���ȷ.
��ѡC.

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�