题目内容
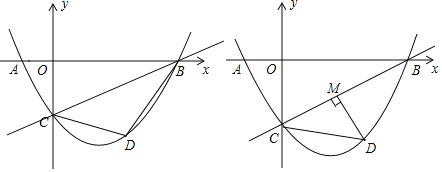
【题目】在矩形ABCD中,AB=8,点H是直线AB边上的一个点,连接DH交直线CB的干点E,交直线AC于点F,连接BF.
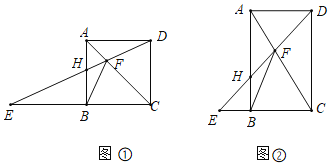
(1)如图①,点H在AB边上,若四边形ABCD是正方形,求证:△ADF≌△ABF;
(2)在(1)的条件下,若△BHF为等腰三角形,求HF的长;
(3)如图②,若tan∠ADH=![]() ,是否存在点H,使得△BHF为等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
,是否存在点H,使得△BHF为等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
【答案】(1)详见解析;(2)8﹣![]() ;(3)存在,详见解析.
;(3)存在,详见解析.
【解析】
(1)根据SAS证明三角形全等即可.
(2)想办法证明∠ADH=30°,求出AH即可解决问题.
(3)如图②中,可以假设AH=4k,AD=3k,DH=5k,因为△BHF是等腰三角形,∠BHF是钝角,推出HF=BH,设BH=HF=x,构建方程组解决问题即可.
(1)证明:如图①中,
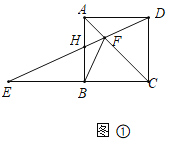
∵四边形ABCD是正方形,
∴AB=AD,∠FAB=∠FAD=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS).
(2)解:如图①中,
∵∠BHF>∠HAD,
∴∠BHF是钝角,
∵△BHF是等腰三角形,
∴BH=FH,
∴∠HBF=∠BFH,
∵△ADF≌△ABF,
∴∠ADF=∠ABF,
∵∠AHD=∠HBF+∠BFH,
∴∠AHD=2∠ADH,
∵∠AHD+∠ADH=90°,
∴∠ADH=30°,
∴AH=ADtan30°=![]() ,
,
∴BH=HF=8﹣![]() .
.
(3)解:如图②中,存在.理由如下:
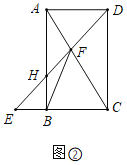
∵四边形ABCD是矩形,
∴AB=CD=8,AB∥CD,∠DAH=90°,
∵tan∠ADH=![]() =
=![]() ,
,
∴可以假设AH=4k,AD=3k,则DH=5k,
∵△BHF是等腰三角形,∠BHF是钝角,
∴HF=BH,设BH=HF=x,
∵AH∥CD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ①,
①,
∵AH+BH=8,
∴4k+x=8 ②,
由①②可得,x=![]() 或
或![]() (舍弃),
(舍弃),
∴存在,该三角形的腰长为![]() .
.

 名校课堂系列答案
名校课堂系列答案