题目内容
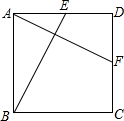
如图1,已知正方形ABCD,将一个45度角∝的顶点放在D点并绕D点旋转,角的两边分别交AB边和BC边于点E和F,连接EF.求证:EF=AE+CF
(1)小明是这样思考的:延长BC到G,使得CG=AE,连接DG,先证△DAE≌△DCG,再证△DEF≌△DGF,请你借助图2,按照小明的思路,写出完整的证明思路.
(2)刘老师看到这条题目后,问了小明两个小问题:①如果正方形的边长和△BEF的面积都等于6,求EF的长②将角∝绕D点继续旋转,使得角∝的两边分别和AB边延长线、BC边的延长线交于E和F,如图3所示,猜想EF、AE、CF三线段之间的数量关系并给予证明.请你帮忙解决.

(1)小明是这样思考的:延长BC到G,使得CG=AE,连接DG,先证△DAE≌△DCG,再证△DEF≌△DGF,请你借助图2,按照小明的思路,写出完整的证明思路.
(2)刘老师看到这条题目后,问了小明两个小问题:①如果正方形的边长和△BEF的面积都等于6,求EF的长②将角∝绕D点继续旋转,使得角∝的两边分别和AB边延长线、BC边的延长线交于E和F,如图3所示,猜想EF、AE、CF三线段之间的数量关系并给予证明.请你帮忙解决.

(1)证明:延长BC到G,使得CG=AE,连接DG,
∵正方形ABCD,
∴AD=DC,∠A=∠BCD=∠DCG=90°,
在△DAE和△DCG中
,
∴△DAE≌△DCG,
∴DE=DG,∠ADE=∠CDG,
∵∠ADC=90°,∠EDF=45°,
∴∠ADE+∠CDF=45°,
∴∠FDC+∠CDG=45°,
∴∠FDG=∠EDF=45°,
在△DEF和△DGF中
,
∴△DEF≌△DGF,
∴EF=FG=CF+CG=CF+AE,
即EF=AE+CF.
(2)①设EF=x,
由(1)知:四边形DEBG的面积=正方形ABCD的面积=36,
又∵△BEF的面积是6,
∴四边形DEFG的面积为30,
∵△DAE≌△DCG,EF=FG=x,
∴△DFG的面积为15,
∴
•6x=15,
解得x=5,
∴EF=5.
②EF=AE-CF,
证明:如图3,延长CF到点G,使得CG=AE,连接DG,
在△DAE和△DCG中
,
∴△DAE≌△DCG,
∴∠CDG=∠ADE,DE=DG,
∵∠ADE+∠CDE=90°,
∴∠CDG+∠CDE=90°,
∵∠EDF=45°,
∴∠GDF=45°,
在△DFE和△DFG中
,
∴△DFE≌△DFG,
∴FE=FG,
∴CG-CF=FG=EF,
∴EF=AE-CF.
∵正方形ABCD,
∴AD=DC,∠A=∠BCD=∠DCG=90°,
在△DAE和△DCG中
|
∴△DAE≌△DCG,
∴DE=DG,∠ADE=∠CDG,

∵∠ADC=90°,∠EDF=45°,
∴∠ADE+∠CDF=45°,
∴∠FDC+∠CDG=45°,
∴∠FDG=∠EDF=45°,
在△DEF和△DGF中
|
∴△DEF≌△DGF,
∴EF=FG=CF+CG=CF+AE,
即EF=AE+CF.
(2)①设EF=x,
由(1)知:四边形DEBG的面积=正方形ABCD的面积=36,
又∵△BEF的面积是6,
∴四边形DEFG的面积为30,
∵△DAE≌△DCG,EF=FG=x,
∴△DFG的面积为15,
∴
| 1 |
| 2 |
解得x=5,
∴EF=5.
②EF=AE-CF,
证明:如图3,延长CF到点G,使得CG=AE,连接DG,
在△DAE和△DCG中
|
∴△DAE≌△DCG,
∴∠CDG=∠ADE,DE=DG,
∵∠ADE+∠CDE=90°,
∴∠CDG+∠CDE=90°,
∵∠EDF=45°,
∴∠GDF=45°,
在△DFE和△DFG中
|
∴△DFE≌△DFG,
∴FE=FG,
∴CG-CF=FG=EF,
∴EF=AE-CF.

练习册系列答案
相关题目