题目内容
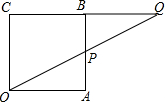
在正方形ABCD中,E、F分别是CB、CD延长线上的点,若EF=BE+DF,求证:∠EAF=135°.


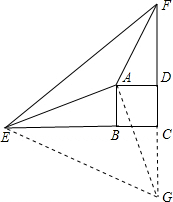
证明:如图,延长DC到G点,使DG=BE,连接AG,GE,
在△AEB和△AGD中,
,
∴△AEB≌△AGD,
∴AE=AG,
∠EAG=∠EAB+∠GAB=∠GAD+∠GAB=90°,
又∵EF=BE+DF=DG+DF=GF,AF=AF,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=
(360°-∠EAG)=135°.
在△AEB和△AGD中,
|
∴△AEB≌△AGD,
∴AE=AG,
∠EAG=∠EAB+∠GAB=∠GAD+∠GAB=90°,
又∵EF=BE+DF=DG+DF=GF,AF=AF,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=
| 1 |
| 2 |


练习册系列答案
相关题目