题目内容
点G是正方形ABCD边AB的中点,点E是射线BC上一点,∠AEF=90°,且EF交正方形外角平分线CF于点F,连接EG.

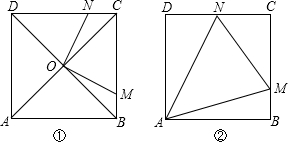
(1)若E为BC的中点(如图1)
①求证:△AEG≌△EFC;
②连接DF,DB,求证:DF⊥BD;
(2)若E是BC延长线上一点(如图2),则线段CF和BE之间存在怎样的数量关系,给出你的结论并证明.

(1)若E为BC的中点(如图1)
①求证:△AEG≌△EFC;
②连接DF,DB,求证:DF⊥BD;
(2)若E是BC延长线上一点(如图2),则线段CF和BE之间存在怎样的数量关系,给出你的结论并证明.
(1)①∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABD=∠BDC=45°.
∵点G、E分别是AB、BC的中点,
∴AG=BG=
AB,BE=CE=
BC,
∴AG=BG=BE=CE.
∴∠BGE=45°,
∴∠AGE=135°.
∵CF平分∠DCN,
∴∠DCF=∠NCF=45°,
∴∠ECF=135°.
∴∠AGE=∠ECF.
∵∠AEF=90°,
∴∠AEB+∠FEN=90°.
∵∠AEB+∠BAE=90°,
∴∠BAE=∠FEC,
在△AEG≌△EFC中,
,
∴△AEG≌△EFC(ASA)
②作FN⊥BC于N,
∴∠FNC=90°,
∴∠ABE=∠ENF.
∵△AEG≌△EFC,
∴AE=EF.
在△ABE和△ENF中,
,
∴△ABE≌△ENF(AAS),
∴FN=BE,
∵∠CFN=45°,
∴CF=
FN.
设AB=CD=AD=CD=2a,
∴BD=2
a,CF=
a,
∴
=
,
=
,
∴
=
,
∵∠ABD=∠FCD=45°,
∴△ABD∽△FCD,
∴∠ADB=∠FDC=45°,
∴∠BDF=90°,
∴DF⊥BD.
(2)CF=
BE.理由:
延长BA到M,使AM=CE,作FG⊥BC的延长线于G,
∴∠FGE=90°,
∴∠ABE=∠FGE.
在Rt△CFG中,由勾股定理.得
∴CF=
FG.
∴∠FGE=∠ABE.
∵∠AEF=90°,
∴∠FEG+∠AEB=90°.
∵∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
∴∠MAE=∠CEF.
∵AB=BC,
∴AB+AM=BC+CE,
即BM=BE.
∴∠M=45°,
∴∠M=∠FCE.
 在△AME和△ECF中,
在△AME和△ECF中,
,
∴AE=EF,∠MAE=∠CEF,
∴∠BAE=∠GEF
在△ABE和△CGF中,
,
∴△ABE≌△CGF(AAS)
∴BE=FG,
∴CF=
BE.
∴AB=BC=CD=AD,∠ABD=∠BDC=45°.
∵点G、E分别是AB、BC的中点,
∴AG=BG=
| 1 |
| 2 |
| 1 |
| 2 |
∴AG=BG=BE=CE.
∴∠BGE=45°,
∴∠AGE=135°.
∵CF平分∠DCN,
∴∠DCF=∠NCF=45°,
∴∠ECF=135°.
∴∠AGE=∠ECF.
∵∠AEF=90°,
∴∠AEB+∠FEN=90°.
∵∠AEB+∠BAE=90°,
∴∠BAE=∠FEC,
在△AEG≌△EFC中,
|
∴△AEG≌△EFC(ASA)
②作FN⊥BC于N,
∴∠FNC=90°,
∴∠ABE=∠ENF.
∵△AEG≌△EFC,
∴AE=EF.
在△ABE和△ENF中,
|
∴△ABE≌△ENF(AAS),
∴FN=BE,
∵∠CFN=45°,
∴CF=
| 2 |
设AB=CD=AD=CD=2a,
∴BD=2
| 2 |
| 2 |
∴
| AB |
| BD |
| ||
| 2 |
| CF |
| CD |
| ||
| 2 |
∴
| AB |
| BD |
| CF |
| CD |
∵∠ABD=∠FCD=45°,
∴△ABD∽△FCD,
∴∠ADB=∠FDC=45°,
∴∠BDF=90°,
∴DF⊥BD.
(2)CF=
| 2 |
延长BA到M,使AM=CE,作FG⊥BC的延长线于G,
∴∠FGE=90°,
∴∠ABE=∠FGE.
在Rt△CFG中,由勾股定理.得
∴CF=
| 2 |
∴∠FGE=∠ABE.
∵∠AEF=90°,
∴∠FEG+∠AEB=90°.
∵∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
∴∠MAE=∠CEF.
∵AB=BC,
∴AB+AM=BC+CE,
即BM=BE.
∴∠M=45°,
∴∠M=∠FCE.
 在△AME和△ECF中,
在△AME和△ECF中,
|
∴AE=EF,∠MAE=∠CEF,
∴∠BAE=∠GEF
在△ABE和△CGF中,
|
∴△ABE≌△CGF(AAS)
∴BE=FG,
∴CF=
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目