Question

如图正方形ABCD中，E为AD边上的中点，过A作AF⊥BE，交CD边于F．求证：点F是CD边的中点．

Answer 1

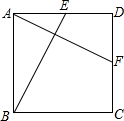
证明：∵∠ABE+∠AEB=90°，∠DAF+∠AEB=90°，
∴∠ABE=∠DAF
在△ABE和△DAF中，

∠ABE=∠DAF ∠FDA=∠EAB AB=DA

，
∴△ABE≌△DAF，
∴DF=AE，
∵E为AD中点，
∴F为CD中点．