题目内容
函数y=-x2+ax+b的图象如图所示．
（1）求a，b的值；
（2）设点P是图象与x轴的另一个交点，求点P的坐标；
（3）求图象的顶点坐标及最大值．
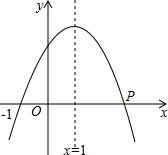
（1）求a，b的值；
（2）设点P是图象与x轴的另一个交点，求点P的坐标；
（3）求图象的顶点坐标及最大值．
（1）∵x=-
=1，
∴a=2，
把（-1，0）代入y=-x2+2x+b得-1-2+b=0，
解得b=3；
（2）抛物线的解析式为y=-x2+2x+3，
当y=0时，-x2+2x+3=0，解得x1=-1，x2=3，
∴P点坐标为（3，0）；
（3）当x=1时，y=-x2+2x+3=-1+2+3=4，
∴图象的顶点坐标为（1，4），最大值为4．
| a |
| 2×(-1) |
∴a=2，
把（-1，0）代入y=-x2+2x+b得-1-2+b=0，
解得b=3；
（2）抛物线的解析式为y=-x2+2x+3，
当y=0时，-x2+2x+3=0，解得x1=-1，x2=3，
∴P点坐标为（3，0）；
（3）当x=1时，y=-x2+2x+3=-1+2+3=4，
∴图象的顶点坐标为（1，4），最大值为4．
练习册系列答案
阅读快车系列答案
相关题目
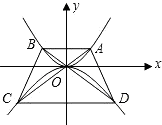抛物线y=-
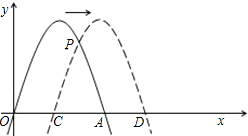们的长度（可用含m的式子表示）；若不存在，请说明理由；
C=OB，抛物线y=（x-2）（x-m）-（p-2）（p-m）（m、p为常数且m+2≥2p＞0）经过A、C两点．
金150万元，请问能否将这30户移民农户全部安置？并说明理由．