题目内容

一座隧道的截面由抛物线和长方形构成，长方形的长为8m，宽为2m，隧道最高点P位于AB的中央且距地面6m，建立如图所示的坐标系．
（1）求抛物线的表达式；
（2）一辆货车高4m，宽2m，能否从该隧道内通过，为什么？
（1）由题意可知抛物线的顶点坐标（4，6），
设抛物线的方程为y=a（x-4）2+6，
又因为点A（0，2）在抛物线上，
所以有2=a（0-4）2+6．
所以a=-
1
4
．
因此有：y=-
1
4
（x-4）2+6．

（2）令y=4，则有4=-
1
4
（x-4）2+6，
解得x1=4+2
2
，x2=4-2
2
，
|x1-x2|=4
2
＞2，
∴货车可以通过．
练习册系列答案
相关题目
已知：抛物线y=ax2+bx+c（a≠0），顶点C（1，-3），与x轴交于A，B两点，A（-1，0）．
（1）求这条抛物线的解析式；
（2）如图，以AB为直径作圆，与抛物线交于点D，与抛物线对称轴交于点E，依次连接A，D，B，E，点P为线段AB上一个动点（P与A，B两点不重合），过点P作PM⊥AE于M，PN⊥DB于N，请判断
PM
BE
+
PN
AD
是否为定值？若是，请求出此定值；若不是，请说明理由；
（3）在（2）的条件下，若点S是线段EP上一点，过点S作FG⊥EP，FG分别与边AE，BE相交于点F，G（F与A，E不重合，G与E，B不重合），请判断
PA
PB
=
EF
EG
是否成立？若成立，请给出证明；若不成立，请说明理由．
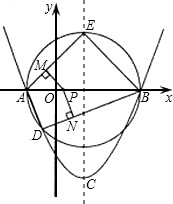
在平面直角坐标系中，已知A（-4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C（0，2），过点C作圆的切线交x轴于点D．
（1）求过A，B，C三点的抛物线的解析式；
（2）求点D的坐标；
（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径；若不存在，请说明理由．
如图，抛物线y=ax2+bx+c与x轴交于点A（-1，0），B（4，0），与y轴交于点C（0，-2）．
（1）求此抛物线的解析式；
（2）若D点在此抛物线上，且AD∥CB，在x轴上是否存在点E，使得以A，D，E为顶点的三角形与△ABC相似？若存在，求出点E的坐标；若不存在，请说明理由；
（3）在（2）的条件下，问在x轴下方的抛物线上，是否存在点P使得△APD的面积与四边形ACBD的面积相等？若存在，求出P点坐标；若不存在，请说明理由．
如图，抛物线y1=-ax2-ax+1经过点P（-
1
2
，
9
8
），且与抛物线y2=ax2-ax-1相交于A，B两点．
（1）求a值；
（2）设y1=-ax2-ax+1与x轴分别交于M，N两点（点M在点N的左边），y2=ax2-ax-1与x轴分别交于E，F两点（点E在点F的左边），观察M，N，E，F四点的坐标，写出一条正确的结论，并通过计算说明；
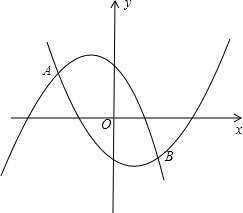（3）设A，B两点的横坐标分别记为xA，xB，若在x轴上有一动点Q（x，0），且xA≤x≤xB，过Q作一条垂直于x轴的直线，与两条抛物线分别交于C，D两点，试问当x为何值时，线段CD有最大值，其最大值为多少？
已知抛物线y=ax2+bx+c与x轴交于A、B两点（点B在点A的右侧，且AB=8），与y轴交于点C，其中点A在x轴的负半轴上，点C在y轴的正半轴上，线段OA、OC的长（OA＜OC）是方程x2-14x+48=0的两个根．
（1）求此抛物线的解析式；
（2）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；
（3）在（2）的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．
已知抛物线y=x2+bx-a2．
（1）请你选定a、b适当的值，然后写出这条抛物线与坐标轴的三个交点，并画出过三个交点的圆；
（2）试讨论此抛物线与坐标轴交点分别是1个，2个，3个时，a、b的取值范围，并且求出交点坐标．
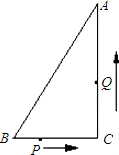如图，在△ABC中，BC=7cm，AC=24cm，AB=25cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，请解答下面的问题，并写出探索的主要过程：
（1）经过多少时间后，P、Q两点的距离为5
2
cm2？
（2）经过多少时间后，S△PCQ的面积为15cm2？
（3）请用配方法说明，何时△PCQ的面积最大，最大面积是多少？
如图，在直角坐标系xOy中，点P为函数y=
1
4
x2在第一象限内的图象上的任一点，点A的坐标为（0，1），直线l过B（0，-1）且与x轴平行，过P作y轴的平行线分别交x轴，l于C，Q，连接AQ交x轴于H，直线PH交y轴于R．
（1）求证：H点为线段AQ的中点；
（2）求证：①四边形APQR为平行四边形；②平行四边形APQR为菱形；
（3）除P点外，直线PH与抛物线y=
1
4
x2有无其它公共点并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网