Question

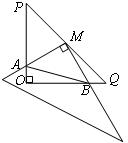
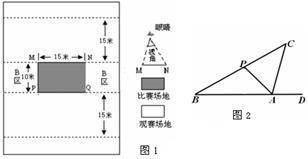
如图是无锡某比赛场馆的平面图，根据距离比赛场地的远近和视角的不同，将观赛场地划分成A、B、C三个不同的票价区．其中与场地边缘MN的视角大于或等于45°，并且距场地边缘MN的距离不超过15米的区域划分为A票区，B票区（如图1所示），剩下的为C票区．

（1）请你利用尺规作图，在观赛场地中，作出A票区所在的区域（只要求作出图形，保留作图痕迹，不要求写作法）；
（2）如果每个座位所占的平均面积是1.2平方米，请估算A票区有多少个座位；
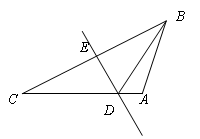
（3）为提高B区观众的观赛效果，举办方将B区用两个大型的支柱AP、AC撑起一定的角度，其横截面如图2所示．若AB=10米，∠B=30°，∠CPA=∠CAD=75°，求CP的长度．（结果保留根号）

Answer 1

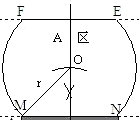
（1）如图所示：

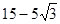
（2）482；（3）

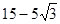
试题分析：（1）可以M、N为圆心，30为半径交于O点如图以线段MN、EF与弧FM、弧EN所围成的区域就是所作的A票区；
（2）求座位就是求三角形EOF，MON和扇形FOM和EON的面积和．那么先求出扇形的半径即可；
（3）先求得BC=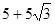，再得到BP=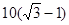，即可求得结果.
（1）如图所示：

（2）由题意得．

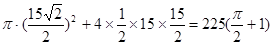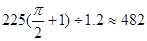
答：A票区有482个座位；
（3）由题意得BC=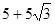，则BP=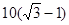
∴CP=
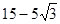
点评：利用数学知识解决实际问题是中学数学的重要内容，解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．