题目内容
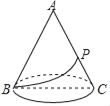
【题目】如图，圆锥的轴截面是边长为6cm的正三角形ABC，P是母线AC的中点，则在圆锥的侧面上从B点到P点的最短路线的长为（ ）
A. 
B. 2 C. 3 D. 4
【答案】C
【解析】
求出圆锥底面圆的周长，则以AB为一边，将圆锥展开，就得到一个以A为圆心，以AB为半径的扇形，根据弧长公式求出展开后扇形的圆心角，求出展开后∠BAC=90°，连接BP，根据勾股定理求出BP即可．
圆锥底面是以BC为直径的圆，圆的周长是 6π，
以AB为一边，将圆锥展开，就得到一个以A为圆心，以AB为半径的扇形，弧长是l=6π，
设展开后的圆心角是n°，则
解得：n=180，
即展开后
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长，
由勾股定理得： 
故选：C．
练习册系列答案
相关题目
