题目内容
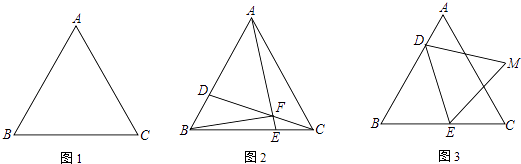
【题目】如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是 . 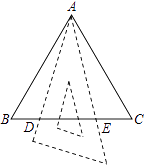
【答案】(2 ![]() ﹣3)a≤DE≤
﹣3)a≤DE≤ ![]() a
a
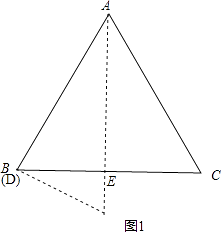
【解析】解:当B、D重合或C、E重合时DE长度最大,如图1,
∵∠BAE=30°,∠AEB=90°,
∴DE= ![]() AB=
AB= ![]() a,
a,
当∠BAD=∠CAE=15°时,DE长度最小,如图2,
作AF⊥BC,且AF=AB,连接DF、CF,
∵AF⊥BC,
∴∠BAF=∠CAF=30°,
∵∠BAD=∠CAE=15°,
∴∠DAH=∠EAH=15°,
∴∠BAD=∠DAH,
在△ADB和△ADF中,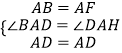 ,
,
∴△ABD≌△ADF,
∴∠B=∠AFD,BD=DF,
∵∠AHB=∠DHF=90°,
∴△ABH∽△DFH,
AB:AH=DF:DH,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DH= ![]() ,其中BD+DH=
,其中BD+DH= ![]() a、AH=
a、AH= ![]() a,
a,
∴DH= ![]() =
= ![]() a
a
∴DE=(2 ![]() ﹣3)a,
﹣3)a,
故DE长度的取值范围是(2 ![]() ﹣3)a≤DE≤
﹣3)a≤DE≤ ![]() a.
a.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目