题目内容
【题目】在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点A旋转60°到△ADE的位置,点C的对应点为E,连接CD,若AC=BC=1,则CD的长为 .
【答案】![]() 或=
或= ![]()
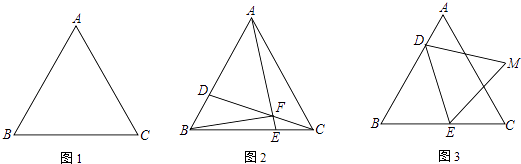
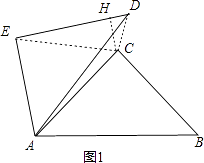
【解析】解:当△ABC绕点A逆时针旋转60°得到△ADE的位置,如图1,作CH⊥ED于H,连结CE,
则∠EAC=60°,∠AED=∠ACB=90°,AE=ED=AC=1,
∴△AEC为等边三角形,
∴∠AEC=60°,EC=CA=1,
∴∠DEC=30°,
在Rt△CEH中,CH= ![]() CE=
CE= ![]() ,EH=
,EH= ![]() CH=
CH= ![]() ,
,
∴DH=ED﹣EH=1﹣ ![]() ,
,
在Rt△CHD中,CD= ![]() =
= ![]() =
= ![]() ;
;
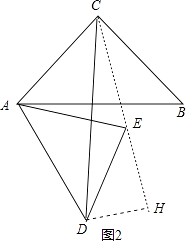
当△ABC绕点A顺时针旋转60°得到△ADE的位置,如图2,连结CE,作DH⊥CE于H,
则∠EAC=60°,∠AED=∠ACB=90°,AE=ED=AC=1,
∴△AEC为等边三角形,
∴∠AEC=60°,EC=CA=1,
∴∠DEC=150°,
∴∠DEH=30°,
在Rt△DEH中,DH= ![]() DE=
DE= ![]() ,EH=
,EH= ![]() DH=
DH= ![]() ,
,
∴CH=CE+EH=1+ ![]() ,
,
在Rt△CHD中,CD= ![]() =
= ![]() =
= ![]() ,
,
纵上所述,CD的长为 ![]() 或=
或= ![]() .
.
所以答案是 ![]() 或=
或= ![]() .
.
【考点精析】关于本题考查的图形的旋转,需要了解每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能得出正确答案.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目