题目内容
【题目】如图,在ABCD中,AE﹕EB=1﹕2, 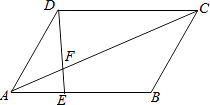
(1)求△AEF与△CDF的周长的比;
(2)如果S△AEF=5cm2 , 求S△CDF .
【答案】
(1)解:∵AE﹕EB=1﹕2,
∴AE﹕AB=1﹕3,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CDF
∴C△AEF﹕C△CDF=AE﹕CD=AE﹕AB=1﹕3,
(2)解:由(1)△AEF∽△CDF
∴S△AEF﹕S△CDF=(AE﹕CD)2,
即5﹕S△CDF=(1﹕3)2
∴S△CDF=45 cm2.
【解析】(1)易证△AEF∽△CDF,由相似三角形的性质:周长之比等于相似比即可求出△AEF与△CDF的周长的比;(2)由(1)可知△AEF∽△CDF,由相似三角形的性质:面积之比等于相似比的平方即可求出问题答案.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目