题目内容
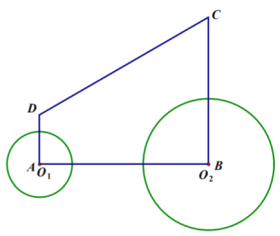
【题目】如图,正方形![]() 的边
的边![]() 在正方形
在正方形![]() 的边
的边![]() 上,连结
上,连结![]() 、
、![]() .
.
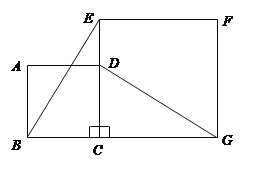
(1)观察猜想![]() 与
与![]() 之间的大小关系,并证明你的结论;
之间的大小关系,并证明你的结论;
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转过程;若不存在,请说明理由.
【答案】(1)BE=DG.理由参见解析;(2)存在.
【解析】
(1)证明线段相等,通常证明线段所在的三角形全等,这里需要证明△BCE≌△DCG即可.
(2)满足旋转后能重合,首先这两个三角形得全等,图中有这样的两个三角形,所以存在.
(1)∵四边形ABCD和四边形ECGF都是正方形,
∴BC=DC,EC=GC,∠ECB=∠GCD=90,
∴△BCE≌△DCG(SAS),
∴BE=DG.
(2)由(1)证明过程知,存在,是Rt△BCE和Rt△DCG.
将Rt△BCE绕点C顺时针旋转90,可与Rt△DCG完全重合.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
【题目】我市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为![]() .
.
(1)根据题意,填写下表:
单人间的房间数 | 10 | … |
| … | 30 |
双人间的房间数 | _________ | … |
| … | 60 |
三人间的房间数 | 70 | … | _________ | … | _________ |
养老床位数 | 260 | … | _________ | … | _________ |
(2)若该养老中心建成后可提供养老床位200个,求![]() 的值;
的值;
(3)求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?