题目内容
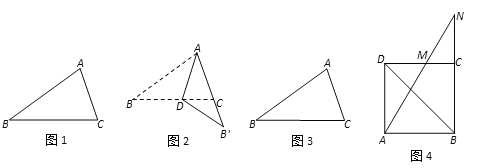
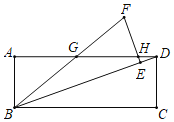
【题目】如图,矩形ABCD中,将△BCD绕点B逆时针旋转得△BEF,其中点C的对应点E恰好落在BD上.BF,EF分别交边AD于点G,H.若GH=4HD,则cos∠DBC的值为_____.
【答案】![]()
【解析】
本题求cos∠DBC的值,即求![]() ,该题思路找出与∠DBC相同的角,由旋转知∠DBC=∠FBE=∠HDE,再证明出∠F=∠GHF,设HD=x,GH=4x,BD=y,则DG=5x,则cos∠DBC=cos∠EDH,
,该题思路找出与∠DBC相同的角,由旋转知∠DBC=∠FBE=∠HDE,再证明出∠F=∠GHF,设HD=x,GH=4x,BD=y,则DG=5x,则cos∠DBC=cos∠EDH,![]() ,∴
,∴![]() ,求出
,求出![]() 即可.
即可.
解:∵将△BCD绕点B逆时针旋转得△BEF,其中点C的对应点E恰好落在BD上.
∴∠FBE=∠DBC,BF=BD,BE=BC,∠BEF=∠C=90°,
∵矩形ABCD中,AD∥BC,
∴∠EDH=∠DBC,
∴∠FBE=∠DBC=∠EDH,
∴BG=DG,
∵GH=4HD,
∴设HD=x,GH=4x,设BE=BC=y,
则BG=DG=5x,
∵∠DHE+∠EDH=90°,∠F+∠FBE=90°,∠FBE=∠EDH,
∴∠F=∠DHE,
∵∠FHG=∠DHE,
∴∠F=∠FHG,
∴GF=GH=4x,
∴BF=BD=9x,DE=9x﹣y,
∵cos∠DBC=cos∠EDH,
∴![]() ,
,
∴![]() ,
,
∴xy=81x2﹣9xy,
∴10xy=81x2,
∴10y=81x,
∴![]() ,,即cos∠DBC=
,,即cos∠DBC=![]() .
.
故答案为:![]() .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】调查作业:了解你所住小区家庭3月份用气量情况.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2—5之间,这300户家庭的平均人数约为3.3.
小天、小东和小芸各自对该小区家庭3月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2、表3,
表1抽样调查小区4户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以上材料回答问题:
(1)小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反应出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处;
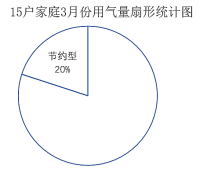
(2)小东将表2中的数据按用气量![]() 大小分为三类;
大小分为三类;
①节约型:![]() ;
;
②居中型:![]() ;
;
③偏高型:![]() ;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
(3)小芸算出表3中3月份平均每人的用量为![]() ,请估计该小区3月份的总用气量.
,请估计该小区3月份的总用气量.