题目内容
【题目】定义:将函数l的图象绕点P(m,0)旋转180°,得到新的函数l'的图象,我们称函数l'是函数关于点P的相关函数.
例如:当m=1时,函数y=(x+1)2+5关于点P(1,0)的相关函数为y=﹣(x﹣3)2﹣5.
(1)当m=0时
①一次函数y=x﹣1关于点P的相关函数为 ;
②点(![]() ,﹣
,﹣![]() )在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
)在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
(2)函数y=(x﹣1)2+2关于点P的相关函数y=﹣(x+3)2﹣2,则m= ;
(3)当m﹣1≤x≤m+2时,函数y=x2﹣mx﹣![]() m2关于点P(m,0)的相关函数的最大值为6,求m的值.
m2关于点P(m,0)的相关函数的最大值为6,求m的值.
【答案】(1)①y=x+1;②a=![]() ;(2)-1;(3)m的值为
;(2)-1;(3)m的值为![]() 或
或![]() .
.
【解析】
(1)①由相关函数的定义,将y=x﹣1旋转变换可得相关函数为y=x+1;
②将(![]() ,﹣
,﹣![]() )代入
)代入 可得a的值,
可得a的值,
(2)两函数顶点关于点P中心对称,可用中点坐标公式获得点P坐标,从而获得m的值;
(3)在相关函数中,以对称轴在给定区间的左侧,中部,右侧,三种情况分类讨论,获得对应的m的值.
解:(1)①∵一次函数y=x﹣1,k=1,过(0,-1)
∴绕点P(0,0)旋转180°后k不变,过(0,1)
∴关于点P的相关函数为y=x+1,
故答案为:y=x+1;
②∵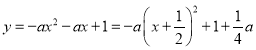 ,
,
∴y=﹣ax2﹣ax+1关于点P(0,0)的相关函数为 ,
,
∵点A(![]() ,﹣
,﹣![]() )在函数
)在函数 的图象上,
的图象上,
∴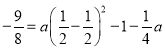 ,
,
解得a=![]() ,
,
(2)∵函数y=(x﹣1)2+2的顶点为(1,2),函数y=﹣(x+3)2﹣2的顶点为(﹣3,﹣2),
这两点关于中心对称,
∴![]() ,
,
∴m=﹣1,
故答案为:﹣1.
(3)∵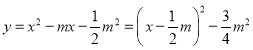 ,
,
∴![]() 关于点P(m,0)的相关函数为
关于点P(m,0)的相关函数为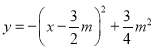 ,
,
①当![]() ,即m≤﹣2时,y有最大值是6,
,即m≤﹣2时,y有最大值是6,
∴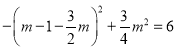 ,
,
∴![]() ,
,![]() (不符合题意,舍去),
(不符合题意,舍去),
②当![]() 时,即﹣2<m≤4时,当
时,即﹣2<m≤4时,当![]() 时,y有最大值是6,
时,y有最大值是6,
∴![]()
∴![]() ,
,![]() (不符合题意,舍去),
(不符合题意,舍去),
③当![]() ,即m>4时,当x=m+2时,y有最大值是6,
,即m>4时,当x=m+2时,y有最大值是6,
∴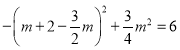 ,
,
∴![]() (不符合题意,舍去),
(不符合题意,舍去),
综上,m的值为![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案