��Ŀ����
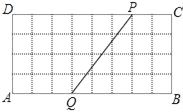
����Ŀ����ͼ1����4��8������ֽ�У�ÿ��С�����εı߳���Ϊ1������P��Q�ֱ�ӵ�D��Aͬʱ���������ƶ�����P���˶��ٶ�Ϊÿ��1����λ����Q���˶��ٶ�Ϊÿ��0.5����λ������P�˶�����Cʱ�������㶼ֹͣ�˶������˶�ʱ��Ϊt��0��t��8����
��1������4��8������ֽͼ2�л���tΪ6��ʱ���߶�PQ�������䳤�ȣ�
��2����tΪ����ʱ����PQB����PQΪ���ĵ��������Σ�

���𰸡���1��PQ=5����2��t=6 ��16��![]() ʱ����PQB����PQΪ���ĵ��������Σ�
ʱ����PQB����PQΪ���ĵ��������Σ�
��������
��1�����ݵ�P���˶��ٶ�Ϊÿ��1����λ����Q���˶��ٶ�Ϊÿ��0.5����λ�����˶�ʱ��tΪ6�룬��ͼ�зֱ���P��Q��λ�ã�Ȼ�������ù��ɶ����������PQ�ij��ȣ�
��2����ʱ��Ϊt������t���ӣ�P�˶���t��Q�˶���![]() t��������ã���PQ=BQ��PQ=BP��������������۷���������ô�.
t��������ã���PQ=BQ��PQ=BP��������������۷���������ô�.
��1����ͼ��ʾ��PQ��Ϊ�˶�6�����߶Σ�
�ɹ��ɶ�����PQ=![]() =5��
=5��
��2����ʱ��Ϊt������t���ӣ�P�˶���t��Q�˶���![]() t��������ã�
t��������ã�
��PQ=BQʱ��
����t��![]() t��2+42=��8��
t��2+42=��8��![]() t��2��
t��2��
���t=6���룩��
��PQ=BPʱ��
��4��![]() t��2+42=��8��
t��2+42=��8��![]() t��2��
t��2��
��ã�t=16��![]() ��
��
�����ϣ�t=6 ��16��![]() ʱ����PQB����PQΪ���ĵ��������Σ�
ʱ����PQB����PQΪ���ĵ��������Σ�

 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�