题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,⊙O交BC于点D,交CA的延长线于点E.过点D作DF⊥AC,垂足为F.

(1)求证:DF为⊙O的切线;
(2)若AB=4,∠C=30°,求劣弧![]() 的长.
的长.
【答案】(1)证明见解析(2)![]()
【解析】(1)连接AD、OD,根据直径所对的圆周角为直角,可得∠ADB=90°,然后根据等腰三角形的性质求出BD=CD,再根据中位线的性质求出OD⊥DF,进而根据切线的判定证明即可;
(2)连接OE,根据三角形的外角求出∠BAE的度数,然后根据圆周角定理求出∠BOE的度数,根据弧长公式求解即可.
(1)连接AD、OD.∵AB是直径,∴∠ADB=90°.
∵AB=AC,∴BD=CD,
又∵OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∵DF⊥AC,∴OD⊥DF
即∠ODF=90°.∴DF为⊙O的切线;
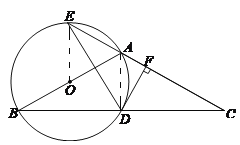
(2)连接OE.∵AB=AC,∴∠B=∠C=30°,∴∠BAE=60°,
∵∠BOE=2∠BAE,∴∠BOE=120°,
∴![]() =
=![]() ·4π=
·4π=![]() π.
π.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】一种树苗,栽种时高度约为80厘米,为研究它的生长情况,测得数据如下表:
(1)此变化过程中_____是自变量,_____是因变量;
(2)树苗高度h与栽种的年数n的关系式为_____;
(3)栽种后_____后,树苗能长到280厘米.
栽种以后的年数n/年 | 高度h/厘米 |
1 | 105 |
2 | 130 |
3 | 155 |
4 | 180 |
… | … |