题目内容
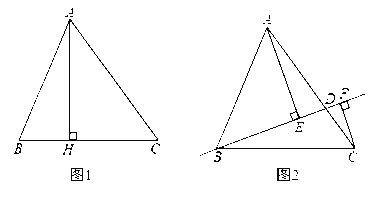
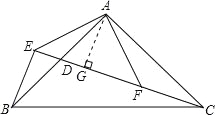
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、通过证△AEB≌△AFC(SAS),得到AE=AF;(2)、如图,过点A作AG⊥EC,垂足为G,通过证△BED≌△AGD(AAS),得到ED=GD,BE=AG,易证CF=BE=AG=GF.因为CD=DG+GF+FC,所以CD=DE+BE+BE,故CD=2BE+DE.
试题解析:(1)、如图,∵∠BAC=90°,AF⊥AE, ∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC, ∵BE⊥CD, ∴∠BEC=90°, ∴∠EBD+∠EDB=∠ADC+∠ACD=90°,
∵∠EDB=∠ADC, ∴∠EBA=∠ACF, ∴在△AEB与△AFC中,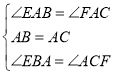 ,
,
∴△AEB≌△AFC(ASA), ∴AE=AF;
(2)、如图,过点A作AG⊥EC,垂足为G. ∵AG⊥EC,BE⊥CE, ∴∠BED=∠AGD=90°,
∵点D是AB的中点, ∴BD=AD. ∴在△BED与△AGD中,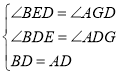 , ∴△BED≌△AGD(AAS), ∴ED=GD,BE=AG, ∵AE=AF ∴∠AEF=∠AFE=45° ∴∠FAG=45° ∴∠GAF=∠GFA, ∴GA=GF, ∴CF=BE=AG=GF, ∵CD=DG+GF+FC, ∴CD=DE+BE+BE, ∴CD=2BE+DE.
, ∴△BED≌△AGD(AAS), ∴ED=GD,BE=AG, ∵AE=AF ∴∠AEF=∠AFE=45° ∴∠FAG=45° ∴∠GAF=∠GFA, ∴GA=GF, ∴CF=BE=AG=GF, ∵CD=DG+GF+FC, ∴CD=DE+BE+BE, ∴CD=2BE+DE.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目