题目内容
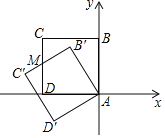
【题目】直线![]() 分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】A
【解析】
试题解析:在△MOC和△NOA中,
 ,
,
∴△MOC≌△NOA,
∴∠CMO=∠ANO,
∵∠CMO+∠MCO=90°,∠MCO=∠NCP,
∴∠NCP+∠CNP=90°,
∴∠MPN=90°
∴MP⊥NP,
在正方形旋转的过程中,同理可证,∴∠CMO=∠ANO,可得∠MPN=90°,MP⊥NP,
∴P在以MN为直径的圆上,
∵M(-4,0),N(0,4),
∴圆心G为(-2,2),半径为2![]() ,
,
∵PG-GC≤PC,
∴当圆心G,点P,C(0,2)三点共线时,PC最小,
∵GN=GM,CN=CO=2,
∴GC= ![]() OM=2,
OM=2,
这个最小值为GP-GC=2![]() -2.
-2.
故选A.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
观察表格:根据表格解答下列问题:
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
(1)![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
(2)在下图的直角坐标系中画出函数![]() 的图象,并根据图象,直接写出当
的图象,并根据图象,直接写出当![]() 取什么实数时,不等式
取什么实数时,不等式![]() 成立;
成立;

(3)该图象与![]() 轴两交点从左到右依次分别为
轴两交点从左到右依次分别为![]() 、
、![]() ,与
,与![]() 轴交点为
轴交点为![]() ,求过这三个点的外接圆的半径.
,求过这三个点的外接圆的半径.