ĚâÄżÄÚČÝ
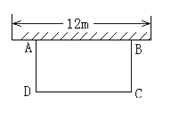
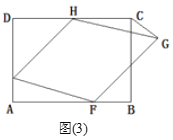
ĄžĚâÄżĄżČçÍźŁŹžŘĐÎֽƏABCDŁŹDCŁ˝8ŁŹADŁ˝6.
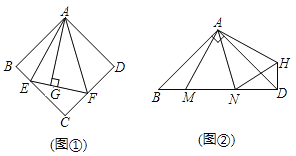
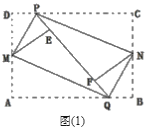
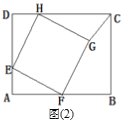
(1)ČçÍź(1)ŁŹľăEÔÚąßADÉĎÇŇAEŁ˝2ŁŹŇÔľăEÎŞśĽľă×÷Őýˇ˝ĐÎEFGHŁŹśĽľăFŁŹHˇÖąđÔÚžŘĐÎABCDľÄąßABŁŹCDÉĎŁŹÁŹ˝ÓCGŁŹÇóĄĎHCGľÄśČĘýŁť
(2)Çë´ÓAĄ˘BÁ˝ĚâÖĐČÎŃĄŇťĚâ˝â´đŁŹÎŇŃĄÔń_____.
A.ČçÍź(2)ŁŹź×͏ѧ°ŃžŘĐÎֽƏABCDľÄËĸö˝ÇĎňÄÚŐŰĆđŁŹÇĄşĂĆ´łÉŇť¸öÎޡěĎśÎŢÖŘľţľÄËÄąßĐÎMPNQŁŹĹМϲ˘ËľĂ÷ËÄąßĐÎMPNQľÄĐÎ×´.
B.ČçÍź(3)ŁŹŇŇ͏ѧ°Ń(1)Öоĥ°Őýˇ˝ĐÎEFGHĄą¸ÄÎŞĄ°ÁâĐÎEFGHĄąŁŹĆäÓŕĚőźţ˛ťąäŁŹ´ËĘąľăGÂäÔÚžŘĐÎABCDľÄÍⲿŁŹŇŃÖŞĄ÷CGHľÄĂćťýĘÇ4ŁŹÇóÁâĐÎEFGHľÄąßł¤ź°Ăćťý.
Ąž´đ°¸Ąż(1)ĄĎHCG= 45ĄăŁť(2)AŁşËÄąßĐÎMPNQľÄĐÎ×´ĘÇžŘĐÎŁŹÖ¤Ă÷źű˝âÎöŁťBŁşÁâĐÎEFGHľÄąßł¤ź°ĂćťýˇÖąđÎŞ4![]() şÍ8+8
şÍ8+8![]() .
.
Ąž˝âÎöĄż
Ł¨1ŁŠĎȸůžÝĚőźţĹĐś¨Ą÷AFEĄŐĄ÷DEHĄŐĄ÷KHGŁŹľĂłöAE=DH=GK=2ŁŹDE=HKŁŹ˝řśřľĂłöGK=CKŁŹź´Ą÷CGKÎŞľČŃüÖą˝ÇČý˝ÇĐÎŁŹžÝ´ËľĂłöĄĎHCGľÄśČĘýŁť
Ł¨2ŁŠ˘ŮČôŃĄAĚ⣏Ôň¸ůžÝŐŰľţľÄĐÔÖĘŁŹÇóľĂĄĎPMQ=ĄĎPME+ĄĎQME=1212ĄĎDME+1212ĄĎAME=1212ĄĎAMD=90ĄăŁŹÍŹŔíżÉľĂŁŹĄĎMQN=90ĄăŁŹĄĎPNQ=90ĄăŁŹ˝řśřľĂłöËÄąßĐÎMPNQľÄĐÎ×´ĘÇžŘĐÎŁť
˘ÚČôŃĄBĚ⣏ÔňĐčŇŞÁŹ˝ÓHFŁŹšýG×÷GPĄÍCDľÄŃÓł¤ĎßÓÚPŁŹÔٸůžÝžŘĐÎşÍÁâĐÎľÄĐÔÖĘŁŹĹĐś¨Ą÷AEFĄŐĄ÷PGHŁ¨AASŁŠŁŹľĂłöPG=AE=2ŁŹÔٸůžÝĄ÷CGHľÄĂćťýĘÇ4ŁŹÇóľĂCHľÄł¤ŁŹ˝řśřÔÚRtĄ÷DEHÖĐŁŹ¸ůžÝš´šÉś¨ŔíľĂłöEHŁŹź´ľĂłöÁâĐÎEFGHľÄąßł¤ŁŹ×îşó¸ůžÝÁâĐÎEFGHľÄĂćťý=2ĄÁĄ÷EFHľÄĂćťý=2ĄÁŁ¨ËÄąßĐÎADHFľÄĂćťý-Ą÷DEHľÄĂćťý-Ą÷AEFľÄĂćťýŁŠŁŹ˝řĐĐźĆËăÇó˝âź´żÉŁŽ
(1)šýľăG×÷GKĄÍCDÓÚľăKŁŹ
ĄßËÄąßĐÎABCDÎŞžŘĐÎŁŹDCŁ˝8ŁŹADŁ˝6ŁŹ
ĄŕĄĎAŁ˝ĄĎDŁ˝ĄĎHKGŁ˝90ĄăŁŹ
ĄßËÄąßĐÎEFGHÎŞŐýˇ˝ĐÎŁŹ
ĄŕĄĎFEHŁ˝ĄĎEHGŁ˝90ĄăŁŹEFŁ˝EHŁ˝HGŁŹ
ĄŕĄĎAFEŁ˝ĄĎDEHŁ˝ĄĎKHGŁŹ
ĄŕĄ÷AFEĄŐĄ÷DEHĄŐĄ÷KHGŁŹ
ĄŕAEŁ˝DHŁ˝GKŁ˝2ŁŹDEŁ˝HKŁŹ
ĄßDCŁ˝8ŁŹADŁ˝6ŁŹ
ĄŕCKŁ˝DCŠDHŁ˝8Š6Ł˝2ŁŹ
ĄŕGKŁ˝CKŁŹ
ĄŕĄĎKCGŁ˝ĄĎCGKŁ˝45ĄăŁŹź´ĄĎHCGľÄśČĘýĘÇ45ĄăŁť
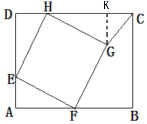
(2)ŃĄAĚ⣏ËÄąßĐÎMPNQľÄĐÎ×´ĘÇžŘĐÎ.Ö¤Ă÷ŁşČçÍź2ŁŹ
ĄßËÄąßĐÎABCDÎŞžŘĐÎŁŹ
ĄŕĄĎAŁ˝ĄĎDŁ˝90ĄăŁŹ
ĄßDMÓëEMÖغϣŹAMÓëEMÖغϣŹ
ĄŕPMĆ˝ˇÖĄĎDMEŁŹQMĆ˝ˇÖĄĎAMEŁŹ
ĄŕĄĎPMQŁ˝ĄĎPME+ĄĎQMEŁ˝![]() ĄĎDME+
ĄĎDME+![]() ĄĎAMEŁ˝
ĄĎAMEŁ˝![]() ĄĎAMDŁ˝90ĄăŁŹ
ĄĎAMDŁ˝90ĄăŁŹ
ÍŹŔíżÉľĂŁŹĄĎMQNŁ˝90ĄăŁŹĄĎPNQŁ˝90ĄăŁŹ
ĄŕËÄąßĐÎMPNQľÄĐÎ×´ĘÇžŘĐÎ.
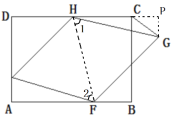
ŃĄBĚ⣏ČçÍź3ŁŹÁŹ˝ÓHFŁŹšýG×÷GPĄÍCDľÄŃÓł¤ĎßÓÚPŁŹĄßËÄąßĐÎABCDÎŞžŘĐÎŁŹĄŕABĄÎCDŁŹĄĎAŁ˝ĄĎDŁ˝90ĄăŁŹĄŕĄĎAFHŁ˝ĄĎPHFŁŹ
ĄßËÄąßĐÎEFGHÎŞÁâĐÎŁŹ
ĄŕEFĄÎHGŁŹEFŁ˝HGŁŹ
ĄŕĄĎ1Ł˝ĄĎ2ŁŹ
ĄŕĄĎAFEŁ˝ĄĎPHGŁŹ
ÓÖĄßGPĄÍDPŁŹ
ĄŕĄĎPŁ˝ĄĎAŁ˝90ĄăŁŹ
ĄŕĄ÷AEFĄŐĄ÷PGH(AAS)ŁŹ
ĄŕPGŁ˝AEŁ˝2ŁŹ
ĄßĄ÷CGHľÄĂćťýĘÇ4ŁŹ
Ąŕ![]() ĄÁHCĄÁPGŁ˝4ŁŹ
ĄÁHCĄÁPGŁ˝4ŁŹ
ĄŕHCŁ˝4ŁŹ
ĄßCDŁ˝8ŁŹADŁ˝6ŁŹAEŁ˝2ŁŹ
ĄŕDHŁ˝8Š4Ł˝4ŁŹDEŁ˝6Š2Ł˝4ŁŹ
ĄŕRtĄ÷DEHÖĐŁŹEHŁ˝4![]() ŁŹ
ŁŹ
ĄŕEFŁ˝4![]() ŁŹź´ÁâĐÎEFGHľÄąßł¤ÎŞ4
ŁŹź´ÁâĐÎEFGHľÄąßł¤ÎŞ4![]() ŁŹ
ŁŹ
ĄŕRtĄ÷AEFÖĐŁŹAFŁ˝2![]() ŁŹ
ŁŹ
ĄŕÁâĐÎEFGHľÄĂćťýŁ˝2ĄÁĄ÷EFHľÄĂćťý
Ł˝2ĄÁ(ËÄąßĐÎADHFľÄĂćťýŠĄ÷DEHľÄĂćťýŠĄ÷AEFľÄĂćťý)
Ł˝2ĄÁ[![]() (DH+AF)ĄÁADŠ
(DH+AF)ĄÁADŠ![]() ĄÁDHĄÁEDŠ
ĄÁDHĄÁEDŠ![]() ĄÁAEĄÁAF]
ĄÁAEĄÁAF]
Ł˝8+8![]() .
.
ĄŕÁâĐÎEFGHľÄąßł¤ź°ĂćťýˇÖąđÎŞ4![]() şÍ8+8
şÍ8+8![]() .
.

ĄžĚâÄżĄżÄł°ŕĘýѧĐËȤХ×éžšýĘĐłĄľ÷˛éŁŹŐűŔíłöÄłÖÖÉĚơÔÚľÚ![]() ĚěľÄĘŰźŰÓëĎúÁżľÄĎŕšŘĐĹϢČçĎÂąíŁş
ĚěľÄĘŰźŰÓëĎúÁżľÄĎŕšŘĐĹϢČçĎÂąíŁş
šŰ˛ěąí¸ńŁş¸ůžÝąí¸ń˝â´đĎÂÁĐÎĘĚ⣺
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
Ł¨1ŁŠ![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
Ł¨2ŁŠÔÚĎÂÍźľÄÖą˝Ç×řąęĎľÖĐťłöşŻĘý![]() ľÄÍźĎ󣏲˘¸ůžÝÍźĎóŁŹÖą˝ÓĐ´łöľą
ľÄÍźĎ󣏲˘¸ůžÝÍźĎóŁŹÖą˝ÓĐ´łöľą![]() ȥʲôʾĘýĘąŁŹ˛ťľČĘ˝
ȥʲôʾĘýĘąŁŹ˛ťľČĘ˝![]() łÉÁ˘Łť
łÉÁ˘Łť

Ł¨3ŁŠ¸ĂÍźĎóÓë![]() ÖáÁ˝˝ťľă´Ó×óľ˝ÓŇŇŔ´ÎˇÖąđÎŞ
ÖáÁ˝˝ťľă´Ó×óľ˝ÓŇŇŔ´ÎˇÖąđÎŞ![]() Ą˘
Ą˘![]() ŁŹÓë
ŁŹÓë![]() ÖὝľăÎŞ
ÖὝľăÎŞ![]() ŁŹÇóšýŐâČý¸öľăľÄÍâ˝ÓÔ˛ľÄ°ëžś.
ŁŹÇóšýŐâČý¸öľăľÄÍâ˝ÓÔ˛ľÄ°ëžś.