题目内容
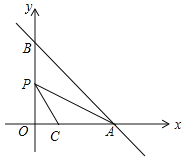
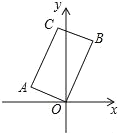
【题目】如图，矩形AOBC中，点A的坐标为（﹣2，1），OB＝5，则点B的坐标为_____．
【答案】（
，2）
【解析】
如图，过点A作AE⊥x轴于E，BF⊥x轴于F，根据矩形的性质以及三角函数的关系得到tan∠OBF＝
，之后利用勾股定理OB2＝OF2+BF2建立方程求解即可
解：如图，过点A作AE⊥x轴于E，BF⊥x轴于F，
∵点A的坐标为（﹣2，1），
∴AE＝1，EO＝2，
∵四边形AOBC是矩形，
∴∠AOB＝90°，
∴∠AOE+∠BOF＝90°，
∵∠BOF+∠OBF＝90°，
∴∠AOE＝∠OBF，
∴tan∠AOE＝tan∠OBF＝，
设OF＝x，则BF＝2x，
∵OB2＝OF2+BF2，
∴25＝5x2，
∴x＝，
∴OF＝，BF＝2，
∴点B的坐标为（，2），
故答案为（，2）．
练习册系列答案
相关题目
【题目】某班数学兴趣小组经过市场调查，整理出某种商品在第
天的售价与销量的相关信息如下表：
观察表格：根据表格解答下列问题：
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
（1）
__________.
_____________.
___________.
（2）在下图的直角坐标系中画出函数
的图象，并根据图象，直接写出当
取什么实数时，不等式
成立；
（3）该图象与轴两交点从左到右依次分别为
、
，与
轴交点为
，求过这三个点的外接圆的半径.
