Question

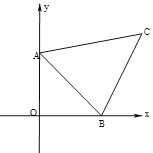
【题目】如图，在平面直角坐标系中，A(0，3)，B(3，0)，C(5，4)，∠OAB=∠OBA=45°，点P为坐标系中第一象限内一点(不与C重合)，若△BAP≌△ABC，则点P坐标为_______.

Answer 1

【答案】(4,5)

【解析】

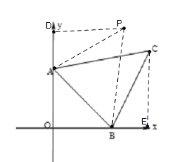
由于△BAP≌△ABC，P在第一象限，AB为公共边，则作如图示意图，过点P作PD垂直于y轴，CE垂直于x轴，利用全等求出DO和DP的长度即可求出点P的坐标.

由于△BAP≌△ABC，P在第一象限，AB为公共边，则作如图示意图，过点P作PD垂直于y轴，CE垂直于x轴，

∴∠PDA=∠CEB=90°，

∵△BAP≌△ABC，

∴AP=BC，∠PAB=∠CBA，

∵∠OAB=∠OBA=45°，

∴∠DAP=∠CBE，

在△DPA和△ECB中

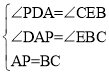
∴△DPA≌△ECB（AAS）

∵A(0，3)，B(3，0)，C(5，4)，

∴BE=DA=2，DP=CE=4，

则DO=5，DP=4，

故点P的坐标为（4,5）.