题目内容
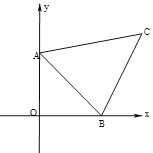
【题目】如图,抛物线![]() 经过
经过![]() 两点,与x轴交于另一点B.点P是抛物线上的动点。
两点,与x轴交于另一点B.点P是抛物线上的动点。
(1)求抛物线的解析式;
(2)是否存在点P,使得△BCP是以BC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)当P运动到第一象限时,过P作直线PM平行y轴,交直线BC于点M。
①求线段PM长度的最大值
②D为平面内任意一点,当线段PM最大时,是否存在以C、P、M、D为顶点的平行四边形。若存在,直接写出所有符合条件的点D坐标.

【答案】(1) ![]() ;(2)见解析;(3) ①4; ②D1
;(2)见解析;(3) ①4; ②D1![]() ,D2
,D2 ![]() ,D3
,D3![]() .
.
【解析】分析: (1)把![]() 两点代入
两点代入![]() 求出抛物线解析式;
求出抛物线解析式;
(2)先确定B(4,0),则判断△OBC为等腰直角三角形得到∠OBC=∠OCB=45°,设![]() 第一种情况,当以C为直角顶点时,过点P作PT⊥y轴,利用TC=TP,可列方程
第一种情况,当以C为直角顶点时,过点P作PT⊥y轴,利用TC=TP,可列方程![]() ,即可求得满足条件的P点坐标;第二种情况,当以B为直角顶点时,过点P作PH⊥x轴,可得PH=HB,从而
,即可求得满足条件的P点坐标;第二种情况,当以B为直角顶点时,过点P作PH⊥x轴,可得PH=HB,从而![]() , 即可求得满足条件的P点坐标;
, 即可求得满足条件的P点坐标;
(3)①求出直线BC解析式, 根据PM平行y轴用二次函数表示P M的长度从而表示出PM的最大值;
②分3种情况:CM为对角线;MP为对角线;CP为对角线.
详解:
(1)将![]() 两点代入到
两点代入到![]() 中得,
中得,
![]()
∴抛物线的解析式为![]() .
.
(2) 存在.
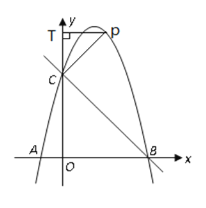
第一种情况,当以C为直角顶点时,过点P作PT⊥y轴,垂足为T。
由抛物线的解析式可得B点坐标为(4,0)
∴OB=OC,∠BOC =90°
∴∠OCB=∠OBC=45°.
∵∠BCP=90°,
∴∠TCP =45°=∠C PT.
∴TC=TP
设![]()
即:![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]()
则P1的坐标是![]() .
.
第二种情况,当以B为直角顶点时,
过点P作PH⊥x轴,垂足为H./span>∵∠CBA=45°,∠CBP=90°,
∴∠OBP=45°.∴∠HPB=45°,
∴PH=HB.
即:![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]()
则P2的坐标是![]() .
.
综上所述,P的坐标是![]() 或
或![]()

(3)① ∵B(4,0), ![]() ∴直线BC解析式为
∴直线BC解析式为![]()
又∵PM平行y轴,设![]()
∴M![]() 。
。
则P M =![]() =
=![]()
∴线段PM长度的最大值为4.
②D1![]() ,D2
,D2 ![]() ,D3
,D3![]()


【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?