题目内容
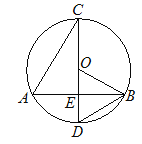
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
![]()
【答案】(1)答案见解析;(2)5.
【解析】
(1)由同弧的圆周角相等即可得出∠ACE=∠DBE,结合∠AEC=∠DEB,即可证出△AEC∽△DEB;(2)设 O的半径为r,则CE=2r-2,根据垂径定理以及三角形相似的性质即可得出关于r的一元一次方程,解方程即可得出r值,此题得解.
本题解析:(1)证明:∵∠AEC=∠DEB,∠ACE=∠DBE,
∴△AEC∽△DEB.
(2)设O的半径为r,则CE=2r2.
∵CD⊥AB,AB=8,
∴AE=BE=![]() AB=4.
AB=4.
∵△AEC∽△DEB,
∴![]() ,即
,即![]() ,
,
解得:r=5.

练习册系列答案
相关题目







