题目内容
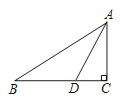
【题目】如图,在![]() ABC中,∠C=90,BD是
ABC中,∠C=90,BD是![]() ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,

(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
【答案】(1)证明见解析;(2)2.
【解析】
(1)考察角平分线定理的性质,及直角三角形全等的判断方法,“HL”;(2)利用全等得到线段AM=BE,AM=AF,利用正方形OECF,得到四边都相等,从而利用OE与BE、AF及AB的关系求出OE的长
解:(1)过点O作OM⊥AB于点M
∵正方形OECF
∴OE=EC=CF=OF,OE⊥BC于E,OF⊥AC于F
∵BD平分∠ABC,OM⊥AB于M,OE⊥BC于E
∴OM=OE=OF
∵OM⊥AB于M, OE⊥BC于E
∴∠AMO=90°,∠AFO=90°
∵![]()
∴Rt△AMO≌Rt△AFO
∴∠MA0=∠FAO
∴点O在∠BAC的平分线上
(2)∵Rt△ABC中,∠C=90°,AC=5,BC=12
∴AB=13
∴BE=BM,AM=AF
又BE=BC-CE,AF=AC-CF,而CE=CF=OE
∴BE=12-OE,AF=5-OE
∴BM+AM=AB
即BE+AF=13
12-OE+5-OE=13
解得OE=2


练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目