题目内容
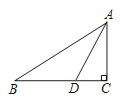
【题目】如图,某高楼OB上有一旗杆CB,我校数学兴趣小组的同学准备利用所学的三角函数知识估测该高楼的高度,由于有其他建筑物遮挡视线不便测量,所以测量员沿坡度i=1:![]() 的山坡从坡脚的A处前行50米到达P处,测得旗杆顶部C的仰角为45°,旗杆底部B的仰角为37°(测量员的身高忽略不计),已知旗杆高BC=15米,则该高楼OB的高度为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
的山坡从坡脚的A处前行50米到达P处,测得旗杆顶部C的仰角为45°,旗杆底部B的仰角为37°(测量员的身高忽略不计),已知旗杆高BC=15米,则该高楼OB的高度为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. 45 B. 60 C. 70 D. 85
【答案】C
【解析】
过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形,
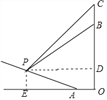
∴PE=OD,
∵AP坡的坡度i=1:![]() ,
,
∴tan∠PAE=![]() ,
,
∴∠PAE=30°,
∴PE=![]() AP=25,
AP=25,
在Rt△PBD中,∠BDP=90°,∠BPD=37°,
∴BD=PDtan∠BPD≈![]() PD,
PD,
在Rt△CPD中,∠CDP=90°,∠CPD=45°,
∴CD=PD,
∵CDBD=BC,
∴PD![]() PD=15,
PD=15,
解得,PD=60,
∴BD=![]() ×60=45,
×60=45,
∴OB=OD+BD=25+45=70,
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目