题目内容
【题目】在平面直角坐标系中,
(1) 取点M(1,0),则点M到直线l: ![]() 的距离为_________,取直线
的距离为_________,取直线![]() 与直线l平行,则两直线距离为_________.
与直线l平行,则两直线距离为_________.
(2) 已知点P为抛物线y=x2-4x的x轴上方一点,且点P到直线l: ![]() 的距离为
的距离为![]() ,求点P的坐标.
,求点P的坐标.
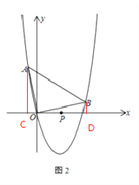
(3) 若直线y=kx+m与抛物线y=x2-4x相交于x轴上方两点A、B(A在B的左边),且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离的最大时直线y=kx+m的解析式.


【答案】(1) ![]() ,
, ![]() ;(2) P(
;(2) P(![]() ,
, ![]() );(3) y=-2x+9.
);(3) y=-2x+9.
【解析】试题分析:(1) 利用直线的正切值即可.(2) 先求出直线与坐标轴的交点坐标,过点E作EG⊥EF交y轴于G,根据已知条件求出EG=![]() ,过点G并且和直线平行的另一条直线就可以画出,根据平行线的性质,求出解析式,联立抛物线解析式即可求出点P的坐标.(3)本题设A(x1,x12-4x)、B(x2,x22-4x),利用一线三等角,得到相似三角形,得AC·BD=OC·OD,求出两根的关系是,再联立方程组,求出直线经过的定点,从而确定距离最远的位置,求出解析式即可.
,过点G并且和直线平行的另一条直线就可以画出,根据平行线的性质,求出解析式,联立抛物线解析式即可求出点P的坐标.(3)本题设A(x1,x12-4x)、B(x2,x22-4x),利用一线三等角,得到相似三角形,得AC·BD=OC·OD,求出两根的关系是,再联立方程组,求出直线经过的定点,从而确定距离最远的位置,求出解析式即可.
试题解析:
解:(1) ![]() ,
, ![]() (利用直线的tan值)
(利用直线的tan值)
(2) 设直线l:y=![]() x-1与x轴、y轴相交于点E、F
x-1与x轴、y轴相交于点E、F
∴E(2,0)、F(0,-1)
过点E作EG⊥EF交y轴于G
∴tan∠EGF=![]()
∴OG=4
∴GE=![]()
∴过点G作直线l的平行线交抛物线于点P,则点P即为所求的点
设直线PG的解析式为![]()
由x2-4x=![]() ,解得
,解得![]()
∴P(![]() ,
, ![]() )
)

(3) 设A(x1,x12-4x)、B(x2,x22-4x)
过点A作AC⊥x轴于C,过点B作BD⊥x轴于D
∴Rt△AOC∽Rt△OBD
∴AC·BD=OC·OD
∴(x12-4x1)(x22-4x2)=-x1x2,x1x2-4(x1+x2)+17=0
联立![]() ,整理得x2-(k+4)x-m=0
,整理得x2-(k+4)x-m=0
∴x1+x2=k+4,x1x2=-m
∴-m-4(k+4)+17=0,m=1-4k
∴直线的解析式为y=kx-4k+1,必过定点Q(4,1)
当点P(2,0)到直线y=kx+m的距离最大时,PQ⊥AB
此时直线的解析式为y=-2x+9.

 53随堂测系列答案
53随堂测系列答案