Question

【题目】菱形ABCD的边长为3，∠BAD＝60°．

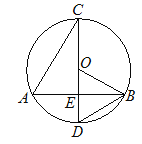
（1）连接AC，过点D作DE⊥AB于点E，DF⊥BC交AC于点F，DE、DF于点M、N．

①依题意补全图1；

②求MN的长；

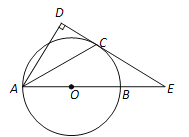
（2）如图2，将（1）中∠EDF以点D为中心，顺时针旋转45°，其两边DE′、DF′分别与直线AB、BC相交于点Q、P，连接QP，请写出求△DPQ的面积的思路．（可以不写出计算结果）

Answer 1

【答案】（1）①答案见解析；②；（2）答案见解析．

【解析】

（1）①根据条件画出图形即可；②连接BD，利用菱形的性质得出△ABD为等边三角形，再利用勾股定理和平行线的性质得出结果即可；（3）由勾股定理和三角形相似的判定及三角形的面积公式求出结果即可.

本题解析：

（1）②证明：连接BD，设BD交AC于O．

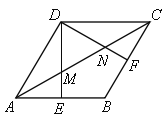
∵在菱形ABCD中，∠DAB＝60°，AD＝AB，∴△ABD为等边三角形，AC⊥BD于点O，∠DAC＝∠DAB＝30°，∴OD＝AD＝．

在Rt△AOD中，OA＝＝，∴AC＝2OA＝．

∵DE⊥AB，∴E为AB中点，∵AE∥CD，∴，同理：，∴M、N是线段AC的三等分点，∴MN＝AC＝．

（2）解：

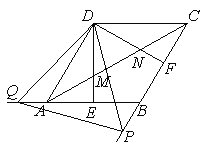
a．在Rt△DCF中，先求出DF的长；

b．在Rt△DFP中，求出DP的长；

c．通过证明△DQA≌△DPB，证明△DPQ是等边三角形；

d．根据DP的长，计算等边三角形的面积．