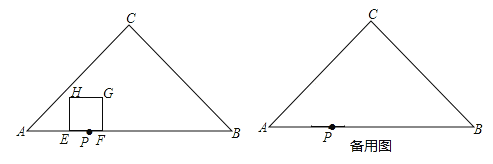题目内容
【题目】已知关于x的方程x2﹣(2k+3)x+k2+2k=0,有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若方程的两实数根x1,x2满足x1x2﹣x12﹣x22=﹣16,求实数k的值.
【答案】(1)k>﹣![]() ;(2)k=1.
;(2)k=1.
【解析】试题分析:(1)根据判别式的意义得到△=(2k+3)2﹣4(k2+2k)>0,然后解不等式即可得到k的范围;
(2)根据根与系数的关系得到x1+x2=2k+3,x1x2=k2+2k,再利用完全平方公式把x1x2﹣x12﹣x22=﹣16变形为(x1+x2)2﹣3x1x2﹣16=0,则(2k+3)2﹣3(k2+2k)﹣16=0,然后解方程求出满足条件的k的值.
试题解析:解:(1)根据题意得:△=(2k+3)2﹣4(k2+2k)>0,解得:k>﹣![]() ;
;
(2)根据题意得:x1+x2=2k+3,x1x2=k2+2k,因为x1x2﹣x12﹣x22=﹣16,所以x1x2﹣[(x1+x2)2﹣2x1x2]=﹣16,即[(x1+x2)2﹣3x1x2﹣16=0,所以(2k+3)2﹣3(k2+2k)﹣16=0,解得:k1=﹣7,k2=1,而k>﹣![]() ,所以k=1.
,所以k=1.

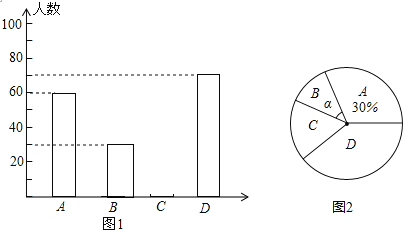
【题目】为进一步推进青少年毒品预防教育“627“工程,切实提高广大青少年识毒、防毒、拒毒的意识和能力,我市高度重视全国青少年禁毒知识竞赛活动.针对某校七年级学生的知识竞赛成绩绘制了如图不完整的统计图表.

知识竞赛成绩频数分布表
组别 | 成绩(分数) | 人数 |
A | 95≤x<100 | 300 |
B | 90≤x<95 | a |
C | 85≤x<90 | 150 |
D | 80≤x<85 | 200 |
E | 75≤x<80 | b |
根据所给信息,解答下列问题.
(1)a=____,b=____.
(2)请求出C组所在扇形统计图中的圆心角的度数.
(3)补全知识竞赛成绩频数分布直方图.
(4)已知我市七年级有180000名学生,请估算全市七年级知识竞赛成绩低于80分的人数.