ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥÷–―ßΈΣΝΥΫβ±Ψ–Θ―ß…ζΤΫΨυΟΩΧλΒΡΩΈΆβΉωΉς“ΒΒΡ ±Φδ«ιΩωΘ§ΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΒς≤ιΘ§≤ΔΫΪΒς≤ιΒΡΫαΙϊΖ÷ΈΣAΓΔBΓΔCΓΔDΥΡΗωΒ»ΦΕΘ®…ηΉωΉς“Β ±ΦδΈΣt–Γ ±Θ§AΘΚtΘΦ1ΘΜBΘΚ1ΓήtΘΦ1.5ΘΜCΘΚ1.5ΓήtΘΦ2ΘΜDΘΚtΓί2Θ©ΗυΨίΒς≤ιΫαΙϊΜφ≥…ΝΥ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°
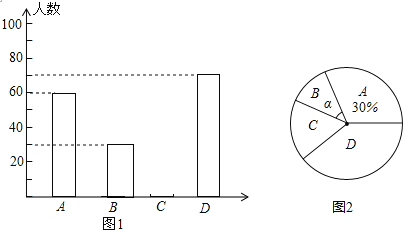
«κΗυΨίΆΦ÷––≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©±Ψ¥ΈΒς≤ι÷–Θ§≥ι»ΓΒΡ―ß…ζ»Υ ΐ « ΘΜ
Θ®2Θ©ΆΦ2÷–ΠΝΒΡΕ» ΐ « Θ§≤Δ≤Ι»ΪΆΦ1Χθ–ΈΆ≥ΦΤΆΦΘΜ
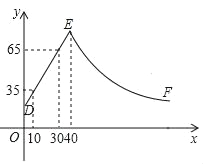
Θ®3Θ©ΗΟ–ΘΙ≤”–2800Οϊ―ß…ζΟϊΘ§«κΙάΦΤΉς“Β ±Φδ≤Μ…Ό”Ύ2–Γ ±ΒΡ»Υ ΐΈΣ ΘΜ
Θ®4Θ©‘Ύ¥Υ¥ΈΒς≤ι÷–Θ§ΦΉΑύ”–2»ΥΤΫΨυΟΩΧλΒΡΉς“Β ±Φδ≥§Ιΐ2–Γ ±Θ§““Αύ”–3Οϊ―ß…ζΤΫΨυΟΩΧλΉς“Β ±Φδ≥§Ιΐ2–Γ ±Θ§œ÷¥”’β5»Υ÷–―Γ»Γ2»Υ≤ΈΦ”ΉυΧΗΜαΘ§«κ”Ο ςΉ¥ΆΦΜρΝ–±μΒΡΖΫΖ®Θ§«σ≥ωΓΑΥυ―ΓΒΡ2»Υά¥Ή‘≤ΜΆ§ΑύΦΕΓ±ΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©200ΘΜΘ®2Θ©54ΓψΘΜΘ®3Θ©980ΘΜΘ®4Θ©![]() Θ°
Θ°
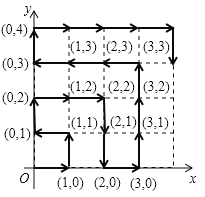
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίBάύΒΡ»Υ ΐΚΆΥυ’ΦΒΡΑΌΖ÷±»Φ¥Ω…«σ≥ωΉή ΐΘΜ
Θ®2Θ©”ΟBΒΡ»Υ ΐ≥ΐ“‘Ήή»Υ ΐ‘Ό≥Υ“‘360ΓψΘ§Φ¥Ω…ΒΟΒΫ‘≤–ΡΫ«ΠΝΒΡΕ» ΐΘ§Ήή»Υ ΐΦθ»ΞAΓΔBΓΔD»Υ ΐΒΟ≥ωCΒΡ»Υ ΐΦ¥Ω…≤Ι»ΪΆΦ–ΈΘΜ
Θ®3Θ©―υ±Ψ÷–DΥυ’Φ±»άΐ≥Υ“‘Ήή»Υ ΐΦ¥Ω…ΒΟΘΜ
Θ®4Θ©œ»…ηΦΉΑύ―ß…ζΈΣA1Θ§A2Θ§““Αύ―ß…ζΈΣB1Θ§B2Θ§B3ΗυΨίΧβ“βΜ≠≥ω ς–ΈΆΦΘ§‘ΌΗυΨίΗ≈¬ ΙΪ ΫΝ– ΫΦΤΥψΦ¥Ω…Θ°
‘ΧβΫβΈωΘΚΫβΘΚΘ®1Θ©Ι≤Βς≤ιΒΡ÷–―ß…ζ ΐ «ΘΚ60Γ¬30%=200Θ®»ΥΘ©Θ°Ι ¥πΑΗΈΣΘΚ200ΘΜ
Θ®2Θ©ΠΝ=![]() ΓΝ360Γψ=54ΓψΘ§CάύΒΡ»Υ ΐ «ΘΚ200©¹60©¹30©¹70=40Θ®»ΥΘ©Θ§»γΆΦ1ΘΚ
ΓΝ360Γψ=54ΓψΘ§CάύΒΡ»Υ ΐ «ΘΚ200©¹60©¹30©¹70=40Θ®»ΥΘ©Θ§»γΆΦ1ΘΚ
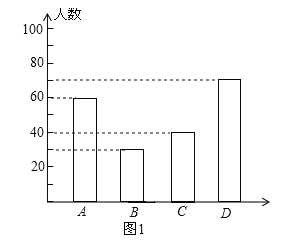
Ι ¥πΑΗΈΣΘΚ54ΓψΘ°
Θ®3Θ©ΙάΦΤΉς“Β ±Φδ≤Μ…Ό”Ύ2–Γ ±ΒΡ»Υ ΐΈΣ![]() ΓΝ2800=980Θ°Ι ¥πΑΗΈΣΘΚ980ΘΜ
ΓΝ2800=980Θ°Ι ¥πΑΗΈΣΘΚ980ΘΜ
Θ®4Θ©…ηΦΉΑύ―ß…ζΈΣA1Θ§A2Θ§““Αύ―ß…ζΈΣB1Θ§B2Θ§B3Θ§

“ΜΙ≤”–20÷÷Β»Ω…ΡήΫαΙϊΘ§Τδ÷–2»Υά¥Ή‘≤ΜΆ§ΑύΦΕΙ≤”–12÷÷Θ§ΓύPΘ®2»Υά¥Ή‘≤ΜΆ§ΑύΦΕΘ©=![]() =
=![]() Θ°
Θ°

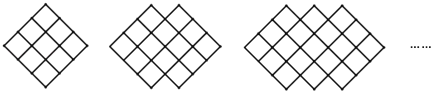
ΓΨΧβΡΩΓΩΈΣΝΥΝΥΫβΫ≠≥«÷–―ß―ß…ζΒΡ…μΗΏ«ιΩωΘ§ΥφΜζΕ‘ΗΟ–ΘΡ–…ζΓΔ≈°…ζΒΡ…μΗΏΫχ––≥ι―υΒς≤ιΘ§“―÷Σ≥ι»ΓΒΡ―υ±Ψ÷–Θ§Ρ–…ζΓΔ≈°…ζΒΡ»Υ ΐœύΆ§Θ§ΗυΨίΥυΒΟ ΐΨίΜφ÷Τ≥…»γœ¬Υυ ΨΒΡΆ≥ΦΤ±μΚΆ»γΆΦΥυ ΨΒΡΆ≥ΦΤΆΦΘ°
Ήι±π | …μΗΏ(cm) |
A | x<150 |
B | 150ΓήxΘΦ155 |
C | 155ΓήxΘΦ160 |
D | 160ΓήxΘΦ165 |
E | xΓί165 |
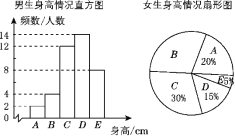
ΗυΨίΆΦ±μ÷–ΧαΙ©ΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
(1)≈°…ζ…μΗΏ‘ΎBΉιΒΡ”–________»ΥΘΜ
(2)‘Ύ―υ±Ψ÷–Θ§…μΗΏ‘Ύ150ΓήxΘΦ155÷°ΦδΒΡΙ≤”–________»ΥΘ§…μΗΏ»Υ ΐΉνΕύΒΡ‘Ύ________Ήι(ΧνΉι±π–ρΚ≈)ΘΜ
(3)“―÷ΣΗΟ–ΘΙ≤”–Ρ–…ζ500»ΥΘ§≈°…ζ480»ΥΘ§«κΙάΦΤ…μΗΏ‘Ύ155ΓήxΘΦ165÷°ΦδΒΡ―ß…ζ”–Εύ…Ό»ΥΘ°
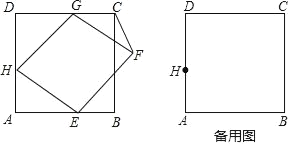
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ΓœCABΘΫ30ΓψΘ§ ACΘΫ4.5cmΘ° M «±ΏAC…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”MBΘ§ΙΐΒψMΉςMBΒΡ¥ΙœΏΫΜAB”ΎΒψNΘ° …ηAM=x cmΘ§AN=y cmΘ°Θ®Β±ΒψM”κΒψAΜρΒψC÷ΊΚœ ±Θ§yΒΡ÷ΒΈΣ0Θ©
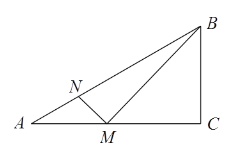
ΧΫΨΩΚ· ΐyΥφΉ‘±δΝΩxΒΡ±δΜ·Εχ±δΜ·ΒΡΙφ¬…Θ°
Θ®1Θ© Ά®Ιΐ»ΓΒψΓΔΜ≠ΆΦΓΔ≤βΝΩΘ§ΒΟΒΫΝΥx”κyΒΡΦΗΉιΕ‘”Π÷ΒΘ§»γœ¬±μΘΚ
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
Θ®“Σ«σΘΚ≤Ι»Ϊ±μΗώΘ§œύΙΊ ΐ÷Β±ΘΝτ“ΜΈΜ–Γ ΐΘ©
Θ®2Θ©Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOyΘ§Οη≥ω“‘≤Ι»ΪΚσΒΡ±μ÷–ΗςΕ‘Ε‘”Π÷ΒΈΣΉχ±ξΒΡΒψΘ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσΘΜ

Θ®3Θ©ΫαΚœΜ≠≥ωΒΡΚ· ΐΆΦœσΘ§ΫβΨωΈ ΧβΘΚΒ±AN=![]() AM ±Θ§AMΒΡ≥ΛΕ»‘ΦΈΣ cmΘ®ΫαΙϊ±ΘΝτ“ΜΈΜ–Γ ΐΘ©Θ°
AM ±Θ§AMΒΡ≥ΛΕ»‘ΦΈΣ cmΘ®ΫαΙϊ±ΘΝτ“ΜΈΜ–Γ ΐΘ©Θ°