题目内容
【题目】如图.在△ABC中,∠C=90°,AC=BC,AB=30cm,点P在AB上,AP=10cm,点E从点P出发沿线段PA以2cm/s的速度向点A运动,同时点F从点P出发沿线段PB以1cm/s的速度向点B运动,点E到达点A后立刻以原速度沿线段AB向点B运动,在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设点E、F运动的时间为t(s)(0<t<20).
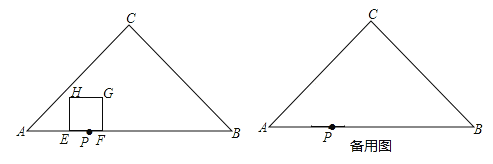
(1)当点H落在AC边上时,求t的值;
(2)设正方形EFGH与△ABC重叠部分的面积为S.①试求S关于t的函数表达式;②以点C为圆心,![]() t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
【答案】(1)t=2s或10s;(2)①S= ;②100cm2.
;②100cm2.
【解析】试题分析:(1)如图1中,当0<t≤5时,由题意AE=EH=EF,即10﹣2t=3t,t=2;如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10;
(2)分四种切线讨论a、如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2.b、如图4中,当2<t≤5时,重叠部分是五边形EFGMN.c、如图5中,当5<t<10时,重叠部分是五边形EFGMN.d、如图6中,当10<t<20时,重叠部分是正方形EFGH.分别计算即可;
②分两种情形分别列出方程即可解决问题.
试题解析:解:(1)如图1中,当0<t≤5时,由题意得:AE=EH=EF,即10﹣2t=3t,t=2
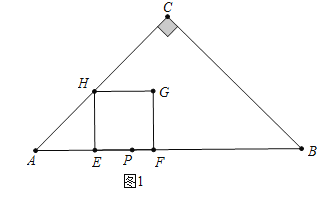
如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10.
综上所述:t=2s或10s时,点H落在AC边上.
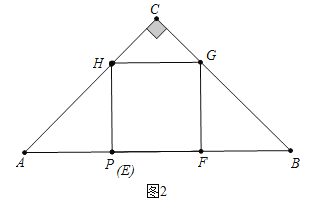
(2)①如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2
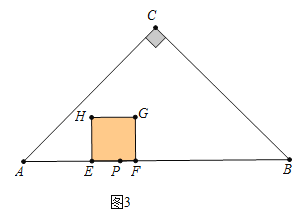
如图4中,当2<t≤5时,重叠部分是五边形EFGMN,S=(3t)2﹣![]() (5t﹣10)2=﹣
(5t﹣10)2=﹣![]() t2+50t﹣50.
t2+50t﹣50.

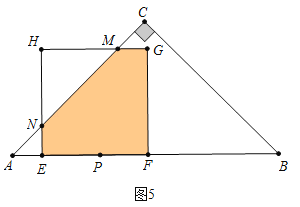
如图5中,当5<t<10时,重叠部分是五边形EFGMN,S=(20﹣t)2﹣![]() (30﹣3t)2=﹣
(30﹣3t)2=﹣![]() t2+50t﹣50.
t2+50t﹣50.
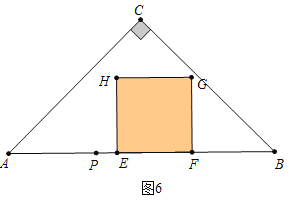
如图6中,当10<t<20时,重叠部分是正方形EFGH,S=(20﹣t)2=t2﹣40t+400.
综上所述:S= .
.
②如图7中,当0<t≤5时,![]() t+3t=15,解得:t=
t+3t=15,解得:t=![]() ,此时S=100cm2,当5<t<20时,
,此时S=100cm2,当5<t<20时,![]() t+20﹣t=15,解得:t=10,此时S=100.
t+20﹣t=15,解得:t=10,此时S=100.
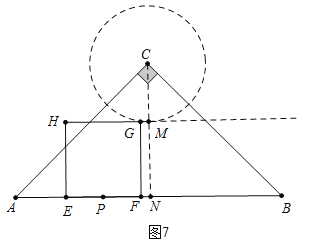
综上所述:当⊙C与GH所在的直线相切时,求此时S的值为100cm2

【题目】新房装修后,某居民购买家用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
垃圾桶 | 15 | ||
鞋架 | 40 | ||
字画 | a | 2 | 90 |
合计 | 5 | 185 | |
(1)居民购买垃圾桶,鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?