题目内容
【题目】已知一次函数的图象经过
，
两点．
（1）求这个一次函数的解析式；
（2）试判断点
是否在这个一次函数的图象上；
（3）求此函数图象与
轴，
轴围成的三角形的面积．
【答案】（1）
；（2）
不在这个一次函数的图象上；（3）函数图象与
轴，
轴围成的三角形的面积=4.
【解析】
（1）利用待定系数法求一次函数解析式；
（2）利用一次函数图象上点的坐标特征进行判断；
（3）先利用一次函数解析式分别求出一次函数与坐标轴的两交点坐标，然后利用三角形面积公式求解．
（1）设一次函数解析式为
，
把
，
代入得
，解得
，
所以一次函数解析式为
；
（2）当
时，
，
所以点
不在这个一次函数的图象上；
（3）当
时，
，则一次函数与轴的交点坐标为
，
当
时，
，解得
，则一次函数与轴的交点坐标为
，
所以此函数图象与轴，轴围成的三角形的面积
．
【题目】已知关于x的方程x2﹣（2k+3）x+k2+2k=0，有两个不相等的实数根x1，x2．
（1）求k的取值范围；
（2）若方程的两实数根x1，x2满足x1x2﹣x12﹣x22=﹣16，求实数k的值．
【题目】为了了解江城中学学生的身高情况，随机对该校男生、女生的身高进行抽样调查，已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制成如下所示的统计表和如图所示的统计图．
组别 | 身高(cm) |
A | x<150 |
B | 150≤x＜155 |
C | 155≤x＜160 |
D | 160≤x＜165 |
E | x≥165 |
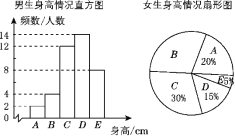
根据图表中提供的信息，回答下列问题：
(1)女生身高在B组的有________人；
(2)在样本中，身高在150≤x＜155之间的共有________人，身高人数最多的在________组(填组别序号)；
(3)已知该校共有男生500人，女生480人，请估计身高在155≤x＜165之间的学生有多少人．
【题目】甲、乙两台机床同时生产一种零件，在5天中，两台机床每天出次品的数量如下表：
甲 | 0 | 1 | 2 | 0 | 2 |
乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差，说法不正确的是
A. 甲、乙的平均数相等B. 甲、乙的众数相等
C. 甲、乙的中位数相等D. 甲的方差大于乙的方差