题目内容
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求完成下面的问题:
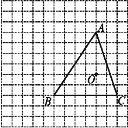
(1)以图中的O为位似中心,将△ABC作位似变换且缩小到原来的一半,得到△A'B'C',再把△A'B'C'绕点B'逆时针旋转90°得到△A″B'C″;
(2)求点A→A'→A″所经过的路线长.
【答案】（1）见解析；（2）2+
【解析】
（1）连接OA，在OA上截取OA′，使OA′=
OA，同理作出B′、C′，顺次连接A′、B′、C′即可；过B′作A″B′⊥A′B′，使A″B′= A′B′，过B′作C″B′⊥B′C′，使C″B′= B′C′，连接A″、B'、C″即可；（2）根据平移性质可得AA′的距离，根据旋转的性质，利用弧长公式可求出弧A′A″的长，即可得答案.
(1) 如图所示：连接OA，在OA上截取OA′，使OA′=OA，同理作出B′、C′，顺次连接A′、B′、C′，△A'B'C'即为所求；过B′作A″B′⊥A′B′，使A″B′= A′B′，过B′作C″B′⊥B′C′，使C″B′= B′C′，连接A″、B'、C″，△A″B'C″即为所求.
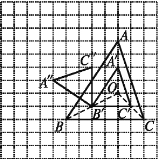
(2)AA′=×4=2，
弧A′A″=
=
∴点A→A'→A″所经过的路线长为：2+.
练习册系列答案
相关题目
